A técnica de voltametria cíclica é um método eletroanalítico largamente usado em química. O método consiste na varredura linear do potencial aplicado num eletrodo de trabalho, medido em relação a um eletrodo de referência. O potencial aplicado pode ser considerado como sinal de entrada e a corrente resultante como o sinal de saída. O registro entrada-saída, denominado de voltamograma, apresenta informações termodinâmicas e cinéticas do processo $($TICIANELLI,2005$)$. A relação entre entrada e saída é dada pela equação integral
$$
\int_0^{\sigma t} \frac{\chi(z)dz}{(\sigma t-z)^{1/2}}=\left[1+\left(\frac{D_0}{D_R}\right)\exp\frac{RT}{nF}(E-E^0)\right]^{-1}
$$
O problema consiste em resolver a Equação acima para vários valores de $(E-E^0)$, obtendo-se os correspodentes valoresde $\chi(\sigma t)$, dos quais pode-se obter a densidade de corrente pela expressão $i=nFC_0^o (\pi D_0\sigma)^{1/2}\chi(\sigma t)$. A função incógnita encontra-se sob o sinal de integral, razão pelo qual definimos o problema como um problema inverso.
Quadratura da equação integral de Volterra
Considere agora equações integrais onde o limite superior da integral é dado por uma função $b(x)$, neste caso, tem-se
$$g(x)=\int_a^{b(x)}K(x,y)f(y)dy$$
Equações deste tipo são conhecidas como equações integrais de Volterra de primeira ordem, em particular, considere aqui equações cujo núcleo é dado por $K(x,y)=(x-y)^{\alpha-1}/\Gamma(\alpha)$ e com os limites de integração dados por $a=0$ e $b(x)=x$, assim
$$g(x)=\frac{1}{\Gamma(\alpha)}\int_0^{x}(x-y)^{\alpha-1}f(y)dy$$
Equações deste tipo também são conhecidas como equações integrais de Caputo de ordem $\alpha$. Semelhante ao que foi feito para as integrais de Fredholm pode-se fazer a quadratura de integrais de Volterra.
Inicialmente, divida a integral acima em $n-1$ intervalos, tal que
$$
g(x) =\frac{1}{\Gamma(\alpha)}\sum_{k=0}^{n-1}\left[\int_{kh}^{(k+1)h}(x-y)^{\alpha-1}f(y)dy\right]
$$
onde $0\leq y\leq x$ e $0\leq x \leq nh$. Para achar $f(y)$ no intervalo entre $y_k$ e $y_{(k+1)h}$ utiliza-se um polinômio interpolador de grau um (reta), tal que
$f(y)\approx f(kh)+\frac{\Delta f}{h}(y-kh)$ em que $\Delta f=f((k+1)h)-f(kh)$. Neste caso, se $y=kh$ então $f(y)=f(kh)$, ou se $y=(k+1)h$ então $f(y)=f((k+1)h)$. Veja que a interpolação por uma reta representa a construção de trapézios retângulos em cada intervalo.
Neste caso, pode-se escrever
$$
g(x)
=\frac{1}{\Gamma(\alpha)}\sum_{k=0}^{n-1}\left[f(kh)\int_{kh}^{(k+1)h}(x-y)^{\alpha-1}dy
+\frac{\Delta f}{h}\int_{kh}^{(k+1)h}(y-kh)(x-y)^{\alpha-1}dy\right]
$$
ou simplemente
$$
g(x)=\sum_{k=0}^{n-1}\left[f(kh)w_{n-k}^\alpha
+\frac{\Delta f}{h}g_{n-k}^\alpha\right]
$$
onde
$$
\begin{array}{ccc}
w_{n-k}^\alpha =\frac{1}{\Gamma(\alpha)}\int_{kh}^{(k+1)h}(x-y)^{\alpha-1}dy
&\hspace{.5cm} \text{e}\hspace{.5cm} &
g_{n-k}^\alpha =\frac{1}{\Gamma(\alpha)}\int_{kh}^{(k+1)h}(y-kh)(x-y)^{\alpha-1}dy
\end{array}
$$
Estas duas integrais podem ser facilmente resolvidas.
Para o peso $w_{n-k}^\alpha$ , tem-se que
$$
\int_{kh}^{(k+1)h}(x-y)^{\alpha-1}dy=
\left.\frac{-(nh-y)^\alpha}{\alpha}\right|_{kh}^{(k+1)h}
=\frac{h^\alpha}{\alpha} [i^\alpha-(i-1)^\alpha]
$$
em que $i=n-k$. Assim,
$$
w_{n-k}^\alpha=\frac{h^\alpha}{\Gamma(\alpha+1)}[i^\alpha-(i-1)^\alpha]
$$
onde $\Gamma(\alpha)\alpha=\Gamma(\alpha+1)$.
A integral para o peso $g_{n-k}^\alpha$ pode ser dividida em dois termos, tal que $I=\Gamma(\alpha)g_{n-k}^\alpha =I_1+I_2$, assim pode-se escrever
$$
\int_{kh}^{(k+1)h}(y-kh)(t-y)^{\alpha-1}dy=
\int_{kh}^{(k+1)h}y(x-y)^{\alpha-1}dy-kh\int_{kh}^{(k+1)h}(x-y)^{\alpha-1}dy
$$
onde, o segundo termo corresponde termo ao resultado apresentado na equação acima multiplicado por $kh$, assim
$$
I_2=kh\int_{kh}^{(k+1)h}(x-y)^{\alpha-1}dy=kh\frac{h^\alpha}{\alpha} [i^\alpha-(i-1)^\alpha]
$$
Para a primeira termo tem-se o resultado
$$
I_1=\int_{kh}^{(k+1)h}y(x-y)^{\alpha-1}dy
= \left.-\frac{(nh-x)^\alpha (nh+y\alpha)}{\alpha(\alpha+1)}\right|_{kh}^{(k+1)h}
=\frac{h^{\alpha+1}}{\alpha(\alpha+1)}\left[
i^\alpha(n+k\alpha)-(i-1)^\alpha(n+k\alpha+\alpha)\right]
$$
Agora, juntando os dois termos, obtém-se
$$
I=I_1+I_2=
\frac{h^{\alpha+1}}{\alpha(\alpha+1)}\left[
i^\alpha(n+k\alpha)-(i-1)^\alpha(n+k\alpha+\alpha)\right]
-kh \frac{h^\alpha}{\alpha} [i^\alpha-(i-1)^\alpha]
$$
Com o objetivo de simplificar a expressão final, a equação acima pode ser reescrita como
$$
I=
\frac{h^{\alpha+1}}{\alpha(\alpha+1)}\left[
i^\alpha(n+k\alpha)-(i-1)^\alpha(n+k\alpha+\alpha)\right]
-k (\alpha+1)\frac{h^{\alpha+1}}{\alpha(\alpha+1)}[i^\alpha-(i-1)^\alpha]
$$
o que nos leva a equação
$$
g_{n-k}^\alpha=\frac{I}{\Gamma(\alpha)} =\frac{h^{\alpha+1}}{\Gamma(\alpha+2)}\left[
i^{\alpha+1}-(i+\alpha)(i-1)^\alpha\right]
$$
onde $i=n-k$.
Portanto, juntando as equações acima tem-se a quadratura da equação integral acima. No entanto, ainda seria interessante colocar este resultado na forma matricial, como foi feito com a equação integral de Fredholm.
Forma matricial da equação integral de Volterra
Usando a definição de $\Delta f$, a equação acima pode ser reescrita como
$$
g(x) =\sum_{k=0}^{n-1}\left[f(kh)w_{n-k}^\alpha
+\frac{f((k+1)h)}{h}g_{n-k}^\alpha-\frac{f(kh)}{h}g_{n-k}^\alpha\right]
$$
o que nos leva a
$$
g(x) =f(0) (w_{n}^\alpha-\frac{g_n^\alpha}{h})+\sum_{k=1}^{n-1}f(kh)\left[w_{n-k}^\alpha
-\frac{g_{n-k}^\alpha}{h}+\frac{g_{n-(k-1)}^\alpha}{h}\right]+f(nh)\frac{g_1^\alpha}{h}
$$
ou simplismente
$$
g(x) =f(0) s_0+\sum_{k=1}^{n-1}f(kh)s_k+f(nh)s_n
$$
onde
$s_0=w_{n}^\alpha-\frac{g_n^\alpha}{h}$,
$s_k=w_{n-k}^\alpha
-\frac{g_{n-k}^\alpha}{h}+\frac{g_{n-(k-1)}^\alpha}{h}$ e
$s_n=\frac{g_1^\alpha}{h}$.
Assim, pode-se screver ${\bf g}={\bf K}{\bf f}$.
Pode-se observar na Equação acima
que o termo do lado esquerdo da igualdade corresponde a integral de Abel, neste caso, a equação acima pode ser escrita em termos da integral fracionária de Riemann-Liouville de ordem 1/2 $($CAMARGO,2015$)$
$$
\Gamma(1/2)[^{RL}D_0^{-1/2} \chi(z)](\sigma t)=\left[1+\left(\frac{D_0}{D_R}\right)\exp\frac{RT}{nF}(E-E^0)\right]^{-1}
$$
No presente trabalho resolvemos a equação acima para construir o voltamograma apresentado na Figura. Este voltamograma foi obtido aplicando o operador $^{RL}D_0^{1/2}$ na Equação (\ref{eq2}), o que fornece o resultado
$$
\chi(\sigma t)=^{RL}D_0^{\alpha}
\left\{\frac{1}{\Gamma(\alpha)}\left[1+\left(\frac{D_0}{D_R}\right)\exp\frac{RT}{nF}(E-E^0)\right]^{-1}\right\}
$$
onde $\alpha=1/2$ para o caso usual. Misceski apresenta uma dedução rigorosa da Equação acima $($MIRCESKI,2009$)$.
Resultados e Discussão
A Figura abaixo apresenta o voltamograma cíclio, conforme previsto pela Equação acima, segundo a teoria de Nicholson e Shain $ ($TICIANELLI,2005$)$. A densidade de corrente foi calculada para $\sigma=3,84$ s, $C_0^o=0,001$ mol/L, $D_0=10^{-6}$cm$^2$/s e $D_0=D_R$.
Neste trabalho, nós usamos um método numérico baseado na regra do trapézio para resolver a Equação acima, quando $\alpha=1/2$. A equação acima sugere uma generalização da teoria de Nicholson e Shain, fazendo $\alpha$ variar entre 0 e 1. O processo analisado envolve difusão de massa o que sugere a existência de efeito de memória, naturalmente introduzido pelo uso de derivadas fracionárias $($MIRCESKI,2009$)$. Resultados calculados para $\alpha\neq 1/2$ são mostrados na Figura.
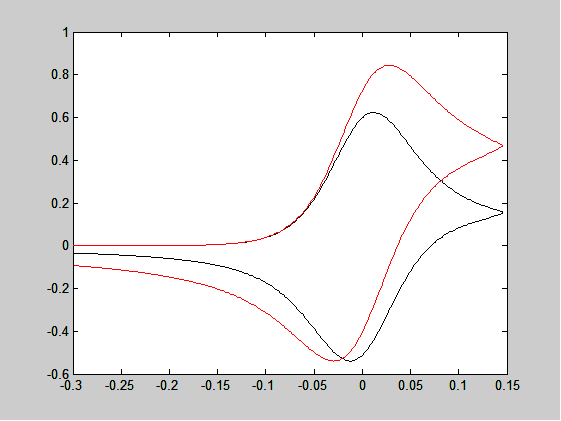
Referências Bibliográficas
CAMARGO, R. F.; OLIVEIRA, E. C. Cálculo Fracionário. São Paulo: LF, 2015.
MIRCESKI, V.; TOMOVSKI, Z. Voltammetry Based on Fractional Diffusion. J. Phys. Chem. B, v.113, p.2794-2799, 2009.
TICIANELLI, A. E.; GONZALES, E. R. Eletroquímica. São Paulo: EDUSP, 2005.

