A lei de arrefecimento de Newton estabelece que a variação de Temperatura ao longo do tempo de um material ao esfriar é proporcional a diferença de temperatura entre o material e a vizinhança, isto é
$\frac{dT(t)}{dt}=\lambda (T(t)-T_a)$
A solução desta equação diferencial pode ser encontrada pelo método operacional usando transformada de Laplace,
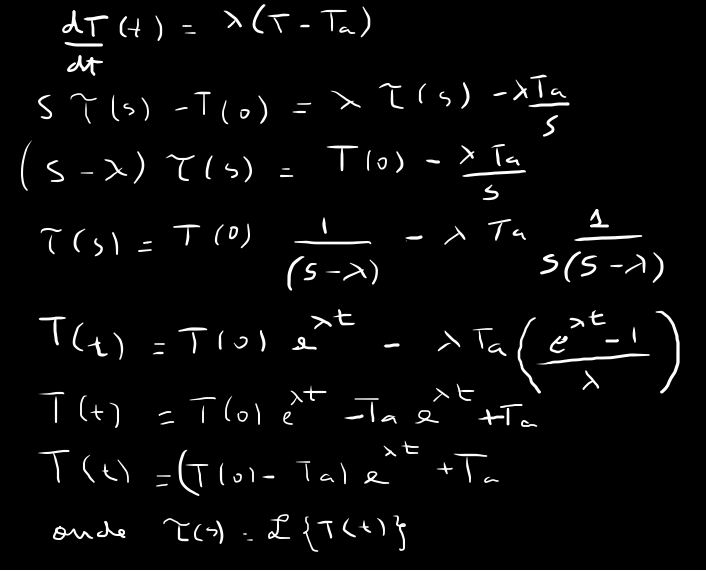
O mesmo método pode ser usado para encontrar a solução da lei de arrefecimento de Newton fracionária
$\frac{d^\alpha T(t)}{dt^\alpha}=\lambda^\alpha (T(t)-T_a)$
onde $0<\alpha<1$,
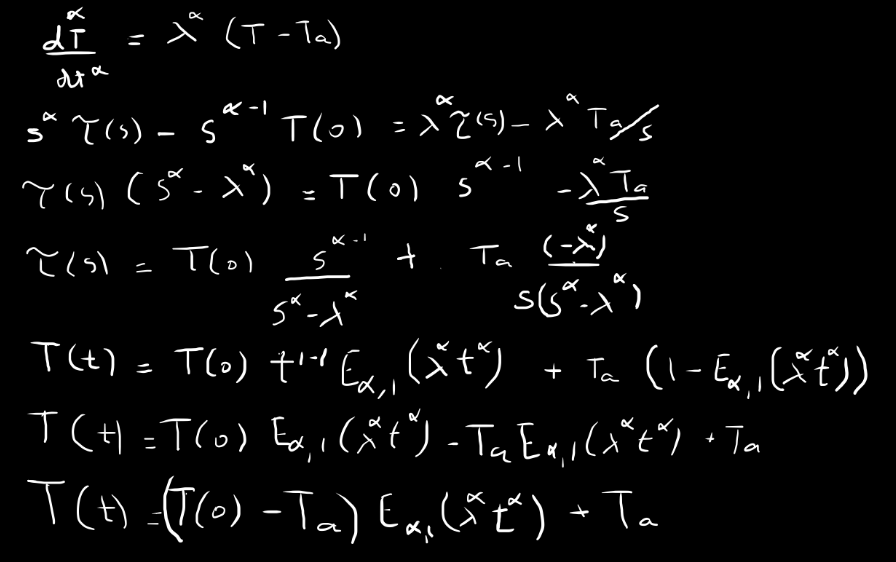
onde $E_{\alpha,1}$ é a função de Mittag-Leffler. Segue abaixo o programa que faz um ajuste dados experimentais obtidos com auxílio de uma placa Arduino$(c)$ pelas equação de ordem fracionária. Os dados experimentais foram obtidos por Higor Monteiro para o seu TCC.

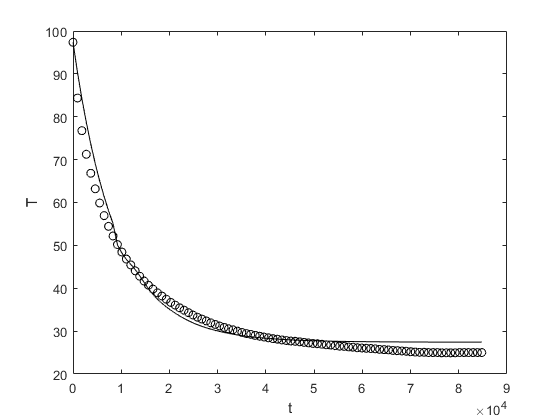
Um resultado inicial é apresentado na figura abaixo $($com $\lambda=1.1160\times 10^{-4}$ e $\alpha=0.9939$$)$. Resultados usando dados parciais e cálculo aproximado da função de Mittag-Leffler não mostraram melhorias significativas. Uma discussão mais aprofundada da questão pode ser encontrada na referência JOURNAL OF APPLIED PHYSICS 123, 064901 (2018). Em breve, irei publicar mais detalhes sobre o Cálculo Fracionário.
function fracnewton
global t T T0 Ta
load -ascii HomeLRN.txt HomeLRN
tdado=HomeLRN(:,1);
mdado=HomeLRN(:,2);
Tdado=HomeLRN(:,3);
Tadado=HomeLRN(:,4);
Udado=HomeLRN(:,5);
inix=find(Tdado==max(Tdado));
ini=max(inix);
r=400;
t0=tdado(ini);
t=tdado(ini:r:end)-t0;
%length(t)
T=Tdado(ini:r:end);
T0=Tdado(ini);
Ta=mean(Tadado(ini:r:end));
m=mdado(ini:r:end);
U=Udado(ini:r:end);
par0=[1e-4,0.9]; %valor inicial dos parâmetros
LB=[1e-5,0];
UB=[1e-3,1];
options=optimoptions('fmincon','Algorithm','interior-point','TolFun', 1e-10, 'TolX', 1e-12);
[par,Feval] = fmincon(@(x) myfun(x),par0,[],[],[],[],LB,UB,[],options);
lambda=par(1)
alpha=par(2)
Feval
Tcala=(T0-Ta)*mlf(alpha,1,-(lambda^alpha)*t.^alpha,12)+Ta;
figure(1)
plot(t,Tcala,'k-',t,T,'ko')
xlabel('t')
ylabel('T')
end
function E=myfun(z)
global t T T0 Ta
lambda=z(1);
alpha=z(2);
Tcala=(T0-Ta)*mlf(alpha,1,-(lambda^alpha)*t.^alpha,12)+Ta;
E=sqrt(sum(((Tcala-T)./T).^2))
end