Cálculo do coeficiente de atividade usando o modelo e-nrtl é baseado na referência AlChE Journal Vol. 28, No. 4, pg 588. Os eletrólitos podem se dissociar parcial ou completamente em solução. Uma mistura de um eletrólito completamente dissociado e um solvente consiste em cátions, ânions e moléculas de solvente. A abordagem adotada no desenvolvimento do modelo é a seguinte. A fórmula estendida de Debye-Huckel proposta por Pitzer (1980) foi usado para representar a contribuição das interações íon-íon de longo alcance, enquanto o modelo nrtl de composição local é usado para representar a contribuição de interações de curto alcance de todos os tipos.
$\ln \gamma_i = \ln \gamma_i^{pdh}+\ln \gamma_i^{lc}$
A subrotina abaixo fornece o resultado para a equação $(5)$ do artigo, juntamente com a equação $(28)$ e $(29)$.
function [lngc,lnga]=lngpdh(s)
global T
Ms=18; Z1=1; Z2=1;
rho=14.9;
c3=exp((T-273.15)/273.15);
Aphi=-61.44534*c3+2.864468*c3.^2+183.5379*log(T/273.15)-0.6820223*(T-273.15)+0.0007875695*(T.^2-(273.15)^2)+58.95788*(273.15./T);
x1=18*s./(1000+18*s); x2=x1;
Ix=.5*(Z1^2*x1+Z2^2*x2);
c1=(2*Z1^2/rho)*log(1+rho*Ix.^.5);
c2=(Z1^2*Ix.^.5-2*Ix.^(3/2))./(1+rho*Ix.^.5);
lngc=-(1000/Ms)^.5*Aphi.*(c1+c2);
c1=(2*Z2^2/rho)*log(1+rho*Ix.^.5);
c2=(Z2^2*Ix.^.5-2*Ix.^(3/2))./(1+rho*Ix.^.5);
lnga=-(1000/Ms)^.5*Aphi.*(c1+c2);
end
O valor de $\rho$ é retirado da referência. A subrotina abaixo fornece o resultado para as equações $(23)$ e $(24)$ do artigo, juntamente com as equações $(10)$, $(19)$, $(20a)$ e $(20b)$ .
function [lngc,lnga]=lnglc(Tcam,Tmca,s)
xa=18*s./(1000+18*s);
xc=xa;
xm=1-(xa+xc);
Za=1; Zc=1;
alpha=.2;
Tam=Tcam; Tcm=Tam;
Gam=exp(-alpha*Tam);
Gcm=Gam;
Tma=Tmca; Tmc=Tma;
Gma=exp(-alpha*Tma);
Gmc=Gma;
lngc=xm.^2*Tcm*Gcm./(xc*Gcm+xa*Gam+xm).^2-Za*xa*Tma.*xm*Gma./(xc+xm*Gma).^2+Zc*xm*Tmc*Gmc./(xa+xm*Gmc)-Zc*Tmc-Gcm*Tcm;
lnga=xm.^2*Tam*Gam./(xc*Gcm+xa*Gam+xm).^2-Zc*xc*Tmc.*xm*Gmc./(xa+xm*Gmc).^2+Za*xm*Tma*Gma./(xc+xm*Gma)-Za*Tma-Gam*Tam;
end
O valor de $\alpha$ é retirado da referência.
Abaixo temos os dados da referência W. J. Hamer and Y. C. Wu, “Osmotic coefficients and mean
activitycoefficients of uni-univalent electrolytes in water at 25◦C,” Journal of Physical and Chemical Reference Data, vol.1, no. 4, pp. 1047–1099, 1972.
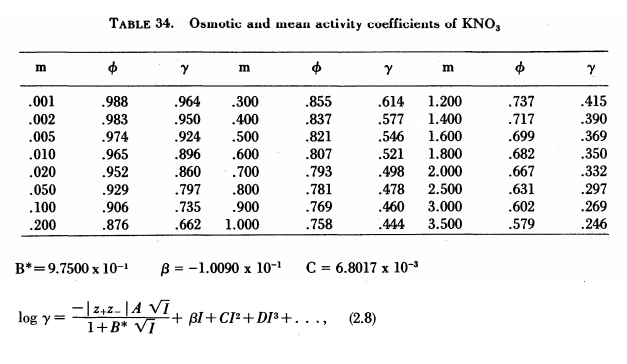
O programa abaixo foi usado para reproduzir estes valores usando o modelo e-nrtl
function kno3part3
clear all
close all
global T
T=298;
%modelo enrtl
Tcam=-3.479;
Tmca=7.673;
i=1;
for s=0.01:.05:3.5;
[lngcpdh,lngapdh]=lngpdh(s);
[lngclc,lngalc]=lnglc(Tcam,Tmca,s);
lngp=lngcpdh+lngclc;
lngm=lngapdh+lngalc;
lngpm=(lngp+lngm)/2;
Ms=18;
m=s;
lngmmolal=lngm-log(1+Ms*(1+1)*m/1000);
gmmolal=exp(lngmmolal);
gpmenrtl(i)=gmmolal;
s0(i)=s;
i=i+1;
end
%T=298 K
%doi:10.5402/2012/730154
D=[0.0012 0.985 0.998 0.991 0.964
0.0021 1.015 1.008 1.011 0.95
0.005 1.003 0.992 0.997 0.924
0.014 0.996 1.003 0.999 0.896
0.021 1.017 0.98 0.998 0.86
0.053 0.96 0.921 0.94 0.797
0.109 0.922 0.871 0.896 0.735
0.191 0.795 0.795 0.795 0.662
0.289 0.753 0.764 0.759 0.614
0.387 0.683 0.71 0.697 0.577
0.516 0.656 0.65 0.653 0.546
0.585 0.643 0.613 0.628 0.521
0.717 0.607 0.572 0.59 0.498
0.781 0.589 0.551 0.57 0.478
0.897 0.581 0.525 0.552 0.46
0.995 0.563 0.486 0.523 0.444
1.175 0.55 0.425 0.483 0.415
1.389 0.528 0.393 0.455 0.39
1.587 0.519 0.371 0.439 0.369
1.798 0.515 0.361 0.431 0.35
1.996 0.512 0.357 0.427 0.332
2.488 0.494 0.33 0.404 0.297
2.98 0.476 0.333 0.398 0.269
3.49 0.452 0.323 0.382 0.246];
s2=D(:,1);
gpmexp1=D(:,4);
%Journal of Physical and Chemical Reference Data, vol.1, no. 4, pp. 1047–1099, 1972.
gpmexp2=D(:,5);
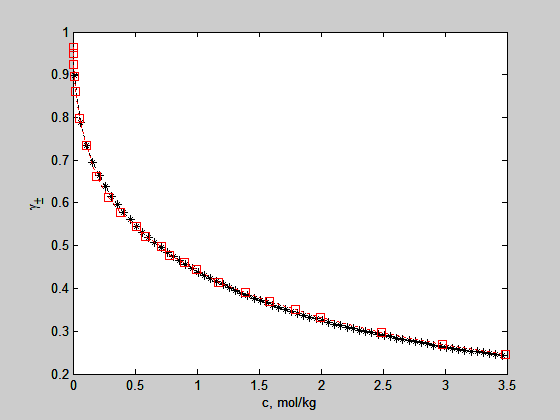
figure
plot(s0,gpmenrtl,'k*:',s2,gpmexp2,'rs:')
ylabel('\gamma_\pm')
xlabel('c, mol/kg')
end
Os parâmetros Tcam=-3.479 e Tmca=7.673 foram retirados do artigo e-nrtl. A comparação é dada na figura abaixo