Este post atualiza os dados apresentados no post do dia 21 de julho (link). Os dados foram atualizados até do dia 05 de setembro. Os ajuste foram feitos usando o modelo de compartimentos denominado SIR com parâmetros dependentes do tempo.
Para descrever de maneira mais apropriada a dinâmica de uma epidemia temos o modelo SIR descrito pelas equações
dS(t)/dt=-b(t) I(t)S(t)/N
dI(t)/dt= b(t) I(t)S(t)/N – g I(t)
dR(t)/dt= g I(t)
onde t é o tempo, S(t) é o número de pessoas suscetíveis no tempo t, I(t) é o número de pessoas infectadas no tempo t e R(t) é o número de pessoas retiradas (que ganharam imunidade por ter tido a doença ou mortas) no tempo t. Os parâmetros b e g representam a taxa de contágio e a taxa de recuperados no período, respectivamente. Neste modelo a população total N=S+I+R é constante.
I(t) = total de casos(t)-R(t)
R(t) = recuperados(t)+mortos(t)
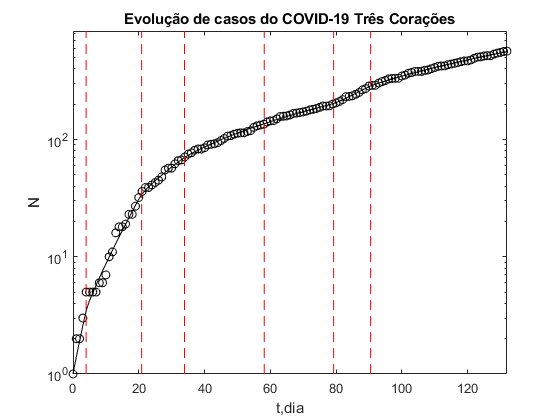
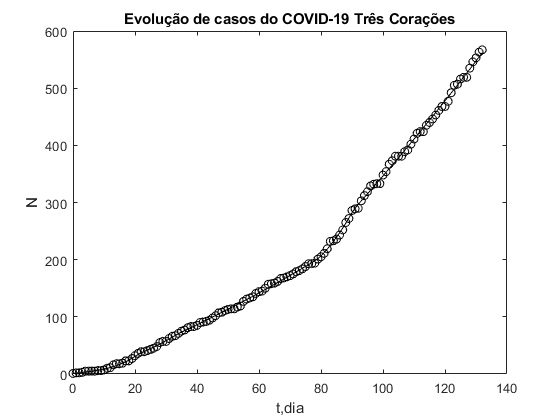
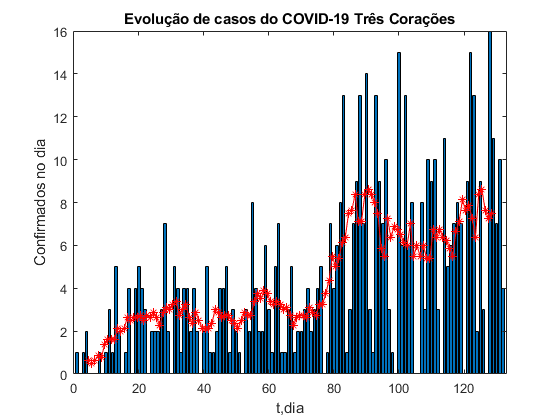
Neste modelo foi incluído uma dependência temporal para o parâmetro b, assim b(t) nas equações acima. A Reprodutibilidade Basal (R0) é dada por b/g, no nosso caso Rt=b(t)/g. O Re, reprodutividade basal equivalente (ou número efetivo de reprodução), é definido por Re=RtS(t)/S(0). O dia 0 é o dia do primeiro caso de COVID-19 confirmado na cidade. O primeiro gráfico apresenta a Reprodutibilidade Basal equivalente (Re) em função do tempo (t,dia), o segundo gráfico apresenta o logaritmo do número de casos confirmados (log N) em função do tempo (t,dia) e o terceiro gráfico número de casos confirmados no dia em função do tempo (t,dia), juntamente com a média móvel – estrelas – (janela de 15 dias). O cálculos foram implementados no MatLab(c). Para estas simulações S0=6.9867e+04 e g=1/14. Teremos o controle da doença quando Re for menor do que 1, neste caso a doença tende a desaparecer da população. Um indicador acima deste valor indica a necessidade de manutenção de medidas de isolamento. O valores apresentados aqui devem ser considerados apenas como indicativo de tendência da evolução da doença.