Na simulação abaixo foram simulados 8 espectros Raman de 8 compostos, sendo dois deles marcadores para uma certa enfermidade, ou da presença de um agente tóxico, ou ainda de um certo agente biológico. Posteriormente, foram gerados 200 espectros esp(:,i), com i=1:200, combinações destes 8 compostos em diferentes concentrações:
esp(:,i)=
z(i)*(c0*spe0+c1*spe1)+c2*spe2+c3*spe3+c4*spe4+c5*spe5+c6*spe6+c7*spe7+c8*spe8;
onde c0, c1, c1, c3, c4, c5, c6, c7 e c8 são concentrações dos 8 compostos na mistura. Para cada mistura as concentrações são geradas aleatoriamente (com distribuição uniforme no intervalo entre 0,5 e 1,5). O parâmetro z(i) é um número aleatório (0 ou 1) com distribuição uniforme (50% e 50%). Este parâmetro controla a presença ou não do agente que queremos investigar. Alguns dos 8 espectros dos 8 compostos são mostrados abaixo:
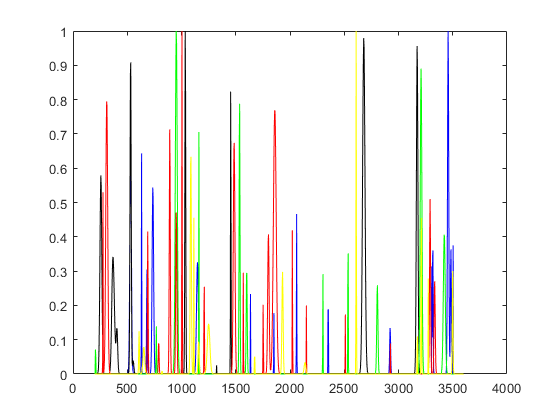
Usando agora o método da análise da componente principal (PCA), já mostrado em post anteriores, temos condições de separar as misturas que possuem o agente que queremos investigar (na figura abaixo marcado de estrela vermelha). Neste caso, os dois grupos são linearmente separáveis.

A implementação feita no MatLab é mostrada abaixo:
close all
clear all
%JUNTANDO
[l,spe0]=simlaesp1(0);
[l,spe1]=simlaesp1(333);
[l,spe2]=simlaesp1(98476482);
[l,spe3]=simlaesp1(23);
[l,spe4]=simlaesp1(4334);
[l,spe5]=simlaesp1(4);
[l,spe6]=simlaesp1(89334);
[l,spe7]=simlaesp1(5464);
[l,spe8]=simlaesp1(433);
figure(1)
plot(l,spe0,'b',l,spe1,'k',l,spe2,'r',l,spe3,'g',l,spe4,'y')
b=1.5; a=.5;
N=200;
for i=1:N
z(i)=randi(2,1)-1;
c0=rand(1)*(b-a)+a;
c1=rand(1)*(b-a)+a;
c2=rand(1)*(b-a)+a;
c3=rand(1)*(b-a)+a;
c4=rand(1)*(b-a)+a;
c5=rand(1)*(b-a)+a;
c6=rand(1)*(b-a)+a;
c7=rand(1)*(b-a)+a;
c8=rand(1)*(b-a)+a;
esp(:,i)=z(i)*(c0*spe0+c1*spe1)+c2*spe2+c3*spe3+c4*spe4+c5*spe5+c6*spe6+c7*spe7+c8*spe8;
end
esp=esp';
x=esp(1,:);
for i=2:N
x=[x; esp(i,:)];
end
[N,M]=size(x);
xm=mean(x); sm=std(x);
for m=1:M
x(:,m)=(x(:,m)-xm(m))./sm(m);
end
[U,S,V]=svd(x); s=diag(S); VT=V'; A=rank(x);
T=U(:,1:A)*S(1:A,1:A);
P=VT(1:A,:);
for i=1:N
for j=1:M
xe(i,j)=sum(T(i,:)*P(:,j));
end
end
e=x-xe;
for i=1:A
Va(i)=100*s(i)^2/sum(s.^2);
Vaa(i)=sum(Va(1:i));
end
disp('Tabela 1')
s(1:A).^2
Va'
Vaa'
for i=1:A
RSSA(i)=sum(s.^2)-sum(s(1:i).^2);
T=U(:,1:i)*S(1:i,1:i);
P=VT(1:i,:);
xi=T*P;
PRESSA(i)=sum(sum((xi-x).^2));
end
disp('Tabela 2')
%s(1:A).^2
RSSA'
PRESSA'
figure(2)
lt=1:N;
plot(lt,T(:,1),'k',lt,T(:,2),'b')
figure(3)
plot(T(:,1),T(:,2),'bo')
hold on
for i=1:N
texto=num2str(l(i));
%text(T(i,1),T(i,2),texto);
end
pos1=find(z==0);
pos2=find(z==1);
plot(T(pos1,1),T(pos1,2),'r*')
plot(T(pos2,1),T(pos2,2),'g*')
figure(4)
plot3(T(:,1),T(:,2),T(:,3),'bo')
hold on
plot3(T(pos1,1),T(pos1,2),T(pos1,3),'r*')
plot3(T(pos2,1),T(pos2,2),T(pos2,3),'g*')
grid on
figure(5)
plot(1:A,P(:,1),'k',1:A,P(:,2),'b')
figure(6)
plot(P(:,1),P(:,2),'bo')

