Para representar graficamente a função y100(r,q,j) seria necessário um espaço de 4 dimensões. Diante disto algumas alternativas são apresentadas na tentativa de visualizar alguns aspectos destas funções
Outro ponto importante é que as autofunções em geral são complexas então para efeito de representação gráfica é conveniente que as funções sejam reais. Já vimos anteriormente que combinações lineares de autofunções de um estado degenerado é uma autofunção deste estado. Neste caso podemos combinar para de funções complexas com o mesmo n, l e |m| para obter funções reais mais convenientes.
As autofunções y21-1(r,q,j) e y211(r,q,j) são estados degenerados, que possuem o mesmo valor de energia, portanto a combinação linear é também uma autofunção com o mesmo valor de energia.
Hy = Ey e Hj = Ej
c = ay+bj
Logo
Hc = H(ay+bj) = aHy+bHj = aEy+Ebj = E(ay+bj) = Ec
Portanto
y211(r,q,j) = -(1/(8Öp)) e-r/2r sen(q)eij
y21-1(r,q,j) = (1/(8Öp)) e-r/2r sen(q)e-ij
y210(r,q,j) =((3/4p))1/2 (1/24)1/2 e-r/2r cos(q)
ypx =(1/Ö2) (y21-1(r,q,j)-y211(r,q,j))
=(1/Ö2) (1/(8Öp)) e-r/2r sen(q) (e-ij– eij)
=(2/Ö2) (1/(8Öp)) e-r/2r sen(q) sen(j)
ypy =(1/Ö2) (y21-1(r,q,j)+y211(r,q,j))
=(1/Ö2) (1/(8Öp)) e-r/2r sen(q) (e-ij+ eij)
=(2/Ö2) (1/(8Öp)) e-r/2r sen(q) cos(j)
ypz = y210(r,q,j) =((3/4p))1/2 (1/24)1/2 e-r/2r cos(q)
ypz = y210(r,q,j) = (1/(16´2p)1/2)e-r/2r cos(q)
ypz = y210(r,q,j) = (1/4)(1/2p)1/2 e-r/2r cos(q)
Onde a denominação px, py e pz se deve a simetria
x = r senq cosj
y = r senq senj
z = r cosq
Do mesmo modo, as funções ydxz, ydx2-y2 etc são obtidas como combinações lineares de outras funções.
Faremos o gráfico de
r(r,q,j) = y*nlm(r,q,j)ynlm(r,q,j)r2sinq drdqdj
Veja que para ilustrar r(r,q,j) seria necessário um espaço de 4 dimensões. Vamos então achar um alternativa, considerando que
òòò r(r,q,j) r2sinq drdqdj = 1
Onde 0£r£¥, 0£j£2p e 0£q£p. Sendo assim
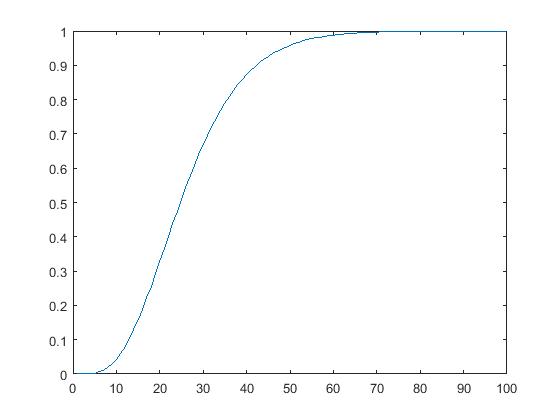
I(r)= 2pò0ròò0p r(r’,q,j)r’2sinqdr’dq
Para o orbital 2pz teremos
function prob
k=1;
for r=0.1:.1:10
p(k) = integral2(@(th,r) funcrhodv(th,r),0,pi,0,r,'RelTol',1e-8,'AbsTol',1e-16);
k=k+1;
end
plot(p)
end
function rhodv=funcrhodv(th,r)
rhodv=2*pi*funcrho(th,r).*r.^2.*sin(th);
end
function rho=funcrho(th,r)
rho=(funcpsi(th,r)).^2;
end
function psi=funcpsi(th,r)
a=0.529177; Z=1;
psi=(1/(4*sqrt(2*pi)))*(Z/a)^(5/2)*exp(-Z*r/(2*a)).*r.*(cos(th));
end
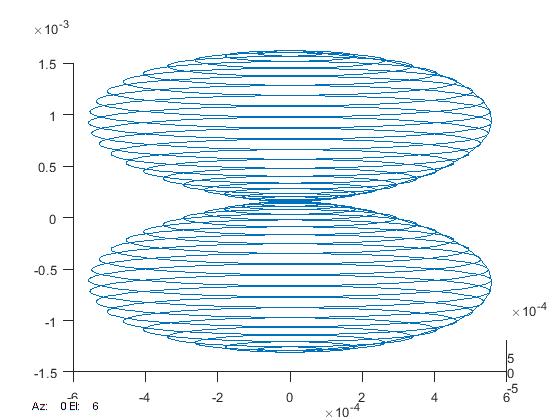
Agora considere que r=r0 tal que
I(r0) = 0,9
teremos então
f(q,j) = r(r0,q,j)
e faremos
x(r0,q,j)= r(r0,q,j) sin(q) cos(j)
y(r0,q,j)= r(r0,q,j) sin(q) sin(j)
z(r0,q,j)= r(r0,q,j) cos(q)
com 0£j£2p e 0£q£p.
%orbital2p
function orbital2p
r = fmincon(@(r) E(r),[1],[],[]);
n=100;
ph=0:2*pi/n:2*pi;
th=0:pi/n:pi;
k=1;
[E(r) r]
for i=1:length(th)
for j=1:length(ph)
x(k)=funcrho(th(i),r)*sin(th(i))*cos(ph(j));
y(k)=funcrho(th(i),r)*sin(th(i))*sin(ph(j));
z(k)=funcrho(th(i),r)*cos(th(i));
k=k+1;
end
end
plot3(x,y,z)
p = integral2(@(th,r) funcrhodv(th,r),0,pi,0,r,'RelTol',1e-8,'AbsTol',1e-16)
end
function Erro=E(r)
p = integral2(@(th,r) funcrhodv(th,r),0,pi,0,r,'RelTol',1e-8,'AbsTol',1e-16);
Erro=(p-0.9)^2;
end
function rhodv=funcrhodv(th,r)
rhodv=2*pi*funcrho(th,r).*r.^2.*sin(th);
end
function rho=funcrho(th,r)
rho=(funcpsi(th,r)).^2;
end
function psi=funcpsi(th,r)
a=0.529177; Z=1;
psi=(1/(4*sqrt(2*pi)))*(Z/a)^(5/2)*exp(-Z*r/(2*a)).*r.*(cos(th));
end