Em geral é possível propor uma geometria levando em conta alguns fatos experimentais. Mas, será possível chegar a uma geometria considerando apenas a estrutura eletrônica do composto (estrutura de Lewis)? Este é o caminho prometido pelo modelo de repulsão dos pares de elétrons da camada de valência, doravante denotado por RPECV.
A Teoria RPECV se baseia no argumento de que os pares de elétrons (ligantes e não ligantes) da camada de valência do átomo central se repelem e que a geometria molecular estável tem como base a geometria eletrônica que minimiza a repulsão entre estes pares de elétrons.
Portanto, para prevermos a geometria de uma molécula, inicialmente precisamos conhecer quantos pares de elétrons estão associados ao átomo central, para tal devemos desenhar a estrutura de Lewis da molécula. Em seguida, a questão passa a ser: – como estes pares de elétrons se distribuem espacialmente de modo que a repulsão seja entre eles a mínima?
Considere uma esfera de raio 1 (unidade arbitrária), onde no centro encontra-se o núcleo do átomo central (carga positiva) e sobre a superfície os pares de elétrons (ligantes e não ligantes) da camada de valência (cargas negativas). Se existem duas cargas negativas qual seria a conformação que minimiza a força repulsão entre elas? A força de repulsão entre as cargas negativas (Força de Coulomb) é dada por
F = ke2/|r12|2
onde |r12| é a distância entre as duas cargas, denominadas de carga 1 e carga 2. Em termos de energia potencial (Energia potencial elétrica ou Energia potencial de Coulomb) temos a expressão
Ep = -ke2/|r12|
Neste caso, buscamos encontrar qual a conformação que minimiza o módulo da energia potencial, |Ep|. Para este exemplo,
r12 = r2 – r1
e
|r12|2 = (r2 – r1).(r2 – r1)=|r2|2+|r1|2-2|r2||r1|cosq
Como |r1|=|r2|=1 chegamos em
|r12|2 = 2(1-cosq)
onde q é o ângulo entre os vetores r1 e r2. Neste caso, F será mínimo quando |r12| for máximo. Tal condição é estabelecida pelas relações:
d|r12|2/dq = 2sinq = 0
d2|r12|2/dq2 = 2cosq> 0
Sendo assim, a questão passa a ser: – qual q que satisfaz as equações acima? O resultado é q = π, é claro! A maior distância entre dois pontos na superfície da esfera ocorre quando os pontos são diametralmente opostos. Mas, a mesma pergunta pode ser feita para 3, 4, 5, 6,… etc cargas sobre a superfície da esfera. E neste caso, um programa simples pode ser feito para este fim.
Um ponto pode ser localizado convenientemente sobre um esfera de raio 1 indicando dois ângulos, q e f. Para o problema sugerido o uso destas coordenadas é mais conveniente. As coordenadas esféricas r=1, q e f, podem ser usadas para determinar sua posição em coordenadas cartesianas através das relações,
x = sin(f)cos(q)
y = sin(f)sin(q)
z = cos(f)
Com as coordenadas (xi,yi,zi) para cada um dos pares de elétrons pode-se calcular as distância entre eles usando a relação,
rij2=(xi-xj)2+(yi-yj)2+(zi-zj)2
como a repulsão total é dada por
F = ke2∑i∑j>i(1/|rij|2)
desejamos a configuração sobre a esfera de N cargas negativas que minimizam F ou de outra forma ∑i∑j>i(1/|rij|)2. Isto formalmente pode ser colocado da seguinte forma
{xi,yi,zi}i=1…N = min ∑i∑j>i(1/|rij|)2
Com os valores {xi,yi,zi} para todo i podemos determinar o ângulo i-O-j formado entre cada par de carga negativa, usando a relação
ang(k)=acos(dot(r(i,:),r(j,:))/norm(r(i,:))*norm(r(j,:)));
onde r=[x ,y, z]. Alguns dos resultados obtidos pela rotina mingeo (abaixo), implementado no MatLab(c), são apresentados abaixo:
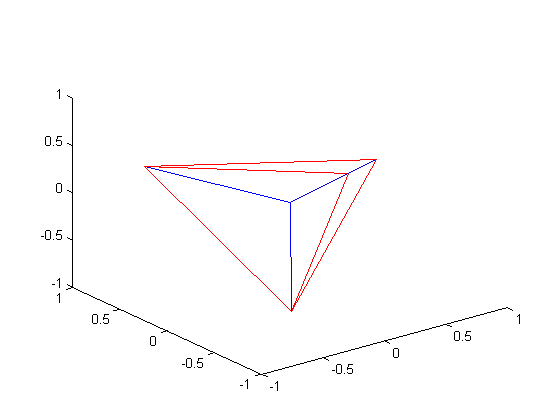
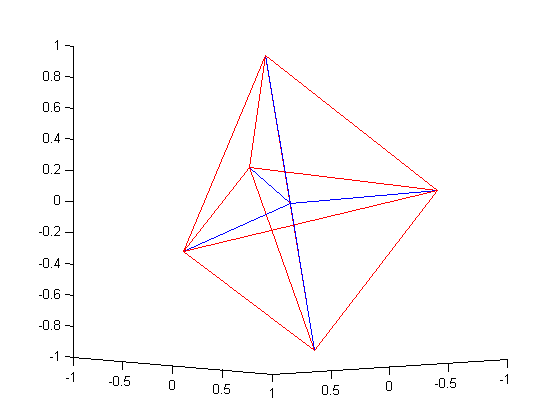
Rotina do matlab: mingeo
function ang=mingeo(a)
global N
N=a;
phi=rand(N,1)*pi;
the=rand(N,1)*2*pi;
x0=[phi;the];
x0
options = optimset('TolFun',1e-16,'TolX',1e-16);
[var,feval] = fminsearch(@(x) func(x),x0,options);
phi=var(1:N);
the=var(N+1:2*N);
x=sin(phi).*cos(the);
y=sin(phi).*sin(the);
z=cos(phi);
r=[x ,y, z];
k=1;
for i=1:N
for j=i+1:N
ang(k)=acos(dot(r(i,:),r(j,:))/norm(r(i,:))*norm(r(j,:)));
k=k+1;
end
end
ang=ang'*180/pi;
figure
for i=1:N
plot3([0,x(i)],[0,y(i)],[0,z(i)])
hold on
end
for i=1:N
for j=i+1:N
plot3([x(j),x(i)],[y(j),y(i)],[z(j),z(i)],'r')
end
end
end
function E=func(var)
global N
phi=var(1:N);
the=var(N+1:2*N);
x=sin(phi).*cos(the);
y=sin(phi).*sin(the);
z=cos(phi);
k=1;
for i=1:N
for j=i+1:N
d(k)=sqrt((x(i)-x(j))^2+(y(i)-y(j))^2+(z(i)-z(j))^2);
k=k+1;
end
end
E=sum(1./d);
end

