Quando experimental function ${\bf \hat f}$ contém erros, algoritmos para filtrar estes erro são, em geral, necessários. Exemplos destes algoritmos foram apresentados em post anteriores. Neste post irei apresentar o filtro de Tikhonov. O método consiste em encontrar a função filtrada de ${\bf f}$ que torna mínimo o funcional $\phi_\lambda({\bf f})$, dado por
$\phi_\lambda({\bf f})=||{\bf f}-{\bf \hat f}||^2+\lambda^2\left(a_0||{\bf f}-{\bf f}_0||^2+a_1||{\bf f}^\prime||^2+a_2||{\bf f}^{\prime\prime}||^2\right)$
Aqui o sinal apóstrofo indica a derivada de ordem 1 da função $f(t)$, o duplo sinal apóstrofo é usado para indicar a deriva de ordem 2 da função $f(t)$. Os parâmetros $a_0$, $a_1$ e $a_2$ são usados para controlar a restrições adicionais ao quadrado da norma do diferença entre a função filtrada e experimental. A função obtida depende do parâmetro de regularização $\lambda$.
Um caminho para encontrar a solução desejada é baseado na definição de $df/dt$ e $d^2f/dt^2$, neste caso
$\left.\frac{df}{dt}\right|_{t_i}=\lim_{\Delta t\rightarrow 0}\frac{\Delta f(t)}{\Delta t}=\frac{f(t_{i}+h)-f(t_i)}{h}$
e
$\left.\frac{d^2f}{dt^2}\right|_{t_i}=\lim_{\Delta t\rightarrow 0}\frac{\Delta f^\prime(t)}{\Delta t}=\frac{f^\prime(t_{i}+h)-f^\prime(t_i)}{h}=\frac{f(t_i+2h)-2f(t_i+h)+f(t_i)}{h^2}$
em que $\Delta t=h$. Então o funcional $\phi_\lambda({\bf f})$ pode ser reescrito como
$\Phi_\lambda({\bf f})=
\sum_i^n ({f}_i-\hat{f}_i)^2
+\lambda^2\left[a_0\sum_i^n(f_i-f_0)^2
+a_1\sum_i^{n-1}\frac{(f_{i+1}-f_i)^2}{h^2}
+a_2\sum_i^{n-2}\frac{(f_{i+2}-2f_{i+1}+f_i)^2}{h^4}\right]$
Agora, derivando o funcional acima em relação a ${f}_i$ obtemos
$\frac{\partial \Phi_\lambda}{\partial f_i}=
2(f_i-\hat{f}_i)
+\lambda^2\left[a_02(f_i-f_0)\right.
-\frac{a_12}{h^2}(f_{i+1}-f_i)
+\frac{a_12}{h^2}(f_i-f_{i-1})\\
\left.+\frac{a_22}{h^4}(f_{i+2}-2f_{i+1}+f_i)
-\frac{a_22}{h^4}(f_{i+1}-2f_{i}+f_{i-1})
+\frac{a_22}{h^4}(f_{i}-2f_{i-1}+f_{i-2})
\right]=0$
Depois de um rearranjo, chegamos em
$\frac{1}{2}\frac{\partial \Phi_\lambda}{\partial f_i}=
(f_i-\hat{f}_i)+\lambda^2a_0f^0_i\\
+\lambda^2\left\{a_0f_i-\frac{a_1}{h^2}(f_{i+1}-2f_i+f_{i-1})
+\frac{a_2}{h^4}(f_{i+2}-4f_{i+1}+6f_i-4f_{i-1}+f_{i-2})\right\}
=0$
Finalmente, no resultado desejado
${\bf f}_\lambda^*=\left[\lambda^2\left\{a_0{\bf H}_0+\frac{a_1}{h^2}{\bf H}_1+\frac
{a_2}{h^4}{\bf H}_2\right\}+{\bf H}_0\right]^{-1}(1+\lambda^2a_0){\bf \hat f}%\left({\bf \hat f}+\lambda^2a_0{\bf \hat f}\right)$
para ${\bf f}_0={\bf \hat f}$, onde
${\bf H}_{1}=\left[\begin{array}{ccccc}
1 & -1 & & & \\
-1 & 2 & -1& &\\
&\ddots &\ddots &\ddots & \\
& & -1 & 2 & -1\\
& & & -1&1\\
\end{array}\right]$
e
${\bf H}_{2}=\left[\begin{array}{ccccccc}
1 & -2 &1 & & & &\\
-2 & 5 & -4& 1& &&\\
1&-4&6&-4&1& &\\
&\ddots &\ddots &\ddots &\ddots &\ddots &\\
&&1 &-4 &6 &-4 &1\\
&&&1& -4 &5 &-2\\
&& & &1 & -2 & 1\\
\end{array}\right]$
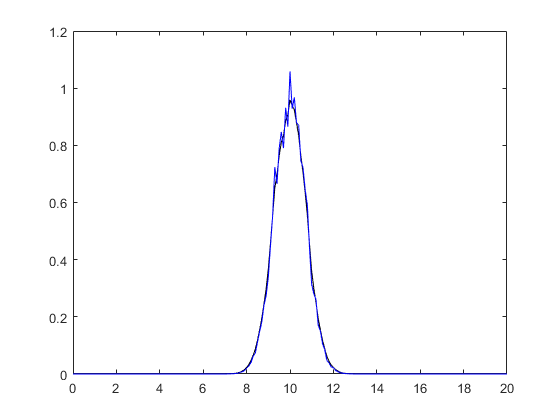
Abaixo apresento a implementação deste algoritmo no MatLab.
function []=filtrotik()
clc
close all
clear all
format long e
rng(0)
x0=10;
y0=1;
s0=1;
x=0:.1:20;x=x';
N=length(x); h=.1;
y=y0*exp(-(x-x0).^2/s0^2);
CV=7/100;
s=CV.*y;
r=randn(size(y)).*s;
Yexp=y+r;
[H0rs,H1rs,H2rs]=matrizes(N);
H0r=H0rs;
H1r=H1rs/h^2;
H2r=H2rs/h^4;
a0=1; a1=1; a2=1;
Y0=Yexp;
expoente=-1.85;
lambda=10^expoente;
q=lambda*(a0*H0r+a1*H1r+0*H2r)+H0r;
r=Yexp+lambda*a0*Y0;
Yfiltro=q\r;
figure(1)
plot(x,Yfiltro,'k-',x,Yexp,'b-')
end
function [H0,H1,H2]=matrizes(n)
H0=eye(n);
H1(1,1)=1;
H1(1,2)=-1;
for i=2:n-1
H1(i,i-1)=-1;
H1(i,i)=2;
H1(i,i+1)=-1;
end
H1(n,n-1)=-1;
H1(n,n)=1;
H2(1,1)=1;
H2(1,2)=-2;
H2(1,3)=1;
H2(2,1)=-2;
H2(2,2)=5;
H2(2,3)=-4;
H2(2,4)=1;
for i=3:n-2
H2(i,i-2)=1;
H2(i,i-1)=-4;
H2(i,i)=6;
H2(i,i+1)=-4;
H2(i,i+2)=1;
end
H2(n-1,n-3)=1;
H2(n-1,n-2)=-4;
H2(n-1,n-1)=5;
H2(n-1,n)=-2;
H2(n,n-2)=1;
H2(n,n-1)=-2;
H2(n,n)=1;
end
As equações deste post foram apresentadas usando o mathjax.

