Suponha os dados consistem de um conjunto de k pontos (xi,yi), com valores de x igualmente espaçados por h. O filtro mais frequentemente para este casos é chamado de Savitzky e Golay, introduzido por Savitzky e Golay em 1964[1]. O filtro consiste em ajustar uma janela de 5 (n) pontos por uma polinômio de grau 3 (m). Primeiro, faremos uma mudança de variável
z=(x-<x>)/h
onde <x> é o valor médio de x na janela s. Logo, z=[-2 -1 0 1 2], para n=5. Um polinômio de grau 3 (m), p3(z)=a0+a1z+a2z2+a3z3, tal que p3(z)=y(z) para os pontos da janela. Assim,
y=Za
onde y=[y1 y2 y3 y4 y5]T, a=[a0 a1 a2 a3 a4]T e Z=[1 -2 4 -8; 1 -1 1 -1; 1 0 0 0; 1 1 1 1; 1 2 4 8]. Z é uma matriz cujos elementos são dados por Zij=zi^(j-1), com 1≤i≤n e 1≤j≤m+1. Neste caso, os coeficientes do polinômio são dados por
a=(ZTZ)-1ZTy
O valor de p3 para o ponto central z=0 é dado por
yfiltro=p3(0)=a0
Segue abaixo a rotina feita no MatLab(c) para implementar o filtro.
[1] Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Abraham Savitzky and M. J. E. Golay. Anal. Chem. 1964, 36, 8, 1627–639. (link)
clc
clear all
close all
%sinal
x0=10; y0=1; s0=1;
x=1:.1:20; x=x';
y=y0*exp(-(x-x0).^2/s0^2);
r=rand(size(y))*.1;
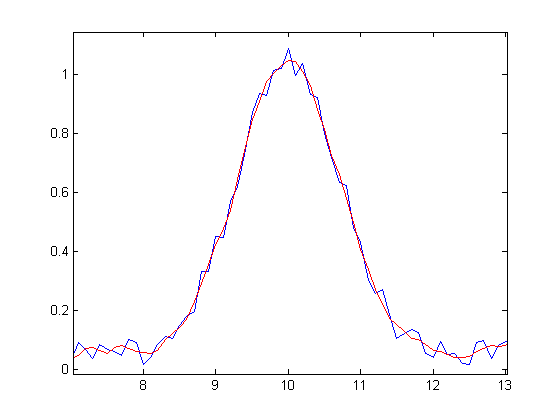
yexp=y+r;
plot(x,yexp,'b-')
%filtro SG
k=length(x); %número de pontos
n=11; %tamanho da janela, deve ser um número menor que k
m=5; %ordem do polinômio, deve ser um número ímpar menor que n
if n>k
disp('Erro')
end
if m/2-fix(m/2) > 0
disp('Erro')
end
if m>5
disp('Erro')
end
w=(n-1)/2;
r=1;
for s=w+1:k-(w+1);
z=-w:1:w;
e=0:1:m;
E=repmat(e,n,1)
Z=repmat(z',1,m+1)
Z=Z.^E;
ys=yexp(s+z);
a=(Z'*Z)\Z'*ys;
yfiltro(r)=a(1);
xfiltro(r)=x(s);
r=r+1;
end
hold on
plot(xfiltro,yfiltro,'r-')

