Filtro de Fourier

Suponha os dados consistem de um conjunto de k pontos (x_i,y_i), com valores de x igualmente espaçados por h. Aplica-se a transformada discreta de Fourier

Y(k)=fft(y(n))=∑_n=1^Ny(n)e^{-j2π(n-1)(k-1)/N}

onde k=1,…,N. No nosso exemplo y corresponde ao valor do sinal no domínio original e Y o valor do sinal no domínio da frequência. O filtro de frequência consiste em eliminar algumas frequências (filtro passa baixa, filtro passa alta, filtro passa banda). O filtro de amplitude consiste em eliminar algumas amplitudes (filtro maior que, filtro menor que). Uma vez feito o corte o sinal é retornado ao domínio original através da transformada inversa

Y*(k)=H(k)Y(k)

f=ifft(Y*(k)) =(1/N)∑_k=1^NY*(k)e^{j2π(n-1)(k-1)/N}

onde n=1,2,…,N. Segue abaixo a rotina feita no MatLab(c) para implementar o filtro.

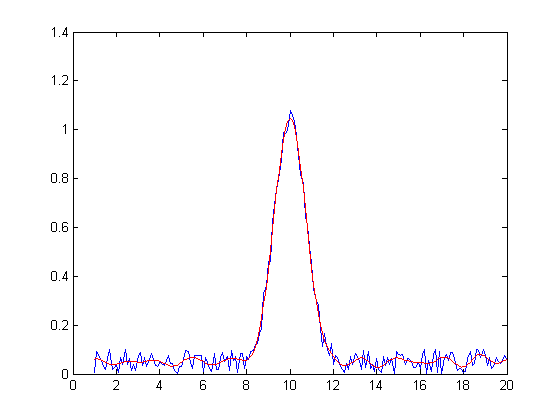
function teste
clc
clear all
close all
%sinal
x0=10; y0=1; s0=1;
x=1:.1:20; x=x';
y=y0*exp(-(x-x0).^2/s0^2);
r=rand(size(y))*.1;
yexp=y+r;
plot(x,yexp,'b-')
yfiltro=filtro(yexp,15,0);
hold on
plot(x,yfiltro,'r-')
end

function yfiltro=filtro(y,k,f1)
m=length(y);
y1 = y; y2 = fliplr(y); yn = [y1 y2];
Y=fft(yn);
%filtro frequência
n=length(Y); H=ones(n,1); r=k+1:n-k; H(r)=0;
Yn=H.*Y(:,1);
%filtro amplitude
Yn2=zeros(1,n); Yn2=abs(Y(r)/max(Y(r))); s=find(Yn2<=f1); Yn(s)=0;
yf=ifft(Yn);
yfiltro=yf(1:m);
end