O nitrato de potássio é um sal bastante solúvel em água, sua solubilidade a 25$^o$C é de aproximadamente de 40 g do sal/100g de água. Outro fato importante é que sua solubidade é bastante afetada pela temperatura, o que motivou sua escolha para este experimento. O experimento descrito é dado a calouros de diferentes cursos na disciplina de Química Geral Experimental, em que a análise dos resultados é limitada a questão se a dissolução do nitrato de potássio é endotérmica ou exotérmica. No entanto, o exemplo é ideal para explorar outras questões, como a não idealidade, modelos para coefiente de atividade e métodos de otimização. A modelagem termodinâmica de sistemas não ideias usando modelos como Debye-Huckel, e-nrtl, etc é um recurso atualmente bastante utilizado em diferentes campos de pesquisa.
Coeficiente de atividade a partir de propriedades termodinâmicas
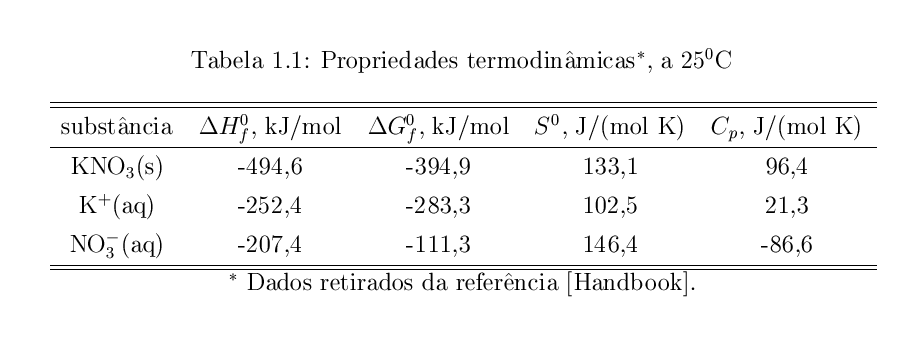
A tabela abaixo apresenta as propriedade termodinâmicas, a 25$^o$C $(T_{ref})$, para as espécies KNO$_3$$(s)$, K$^+$$(aq)$ e NO$_3^-$$(aq)$, que foram retidas do CRC HandBook $($páginas 865, 930 e 931$)$. Estes dados serão usados para calcular a solubilidade em diferentes temperaturas.
Para a dissolução do KNO$_3$ tem-se o equilíbrio
$KNO_3(s)= K^+(aq) + NO_3^-(aq)$
cuja constante $K_{ps}$ é dada por $($equação 8 da referência $[1])$
$K_{ps}(T_{ref}) = e^{-\Delta G_{diss}^0(T_{ref})/RT_{ref}}$
em que
$\Delta G_{diss}^0(T_{ref}) = \sum\Delta G_f^0(prod)-\sum\Delta G_f^0(reag)=$
=-283.3-111.3+394.9 = 0.3 kJ/mol= 300 J/mol
Os valores de $K_{ps}$ para outras temperaturas são dados por $($equação 14 da referência $[1])$
$\ln K_{ps}(T^\prime)=$
$=\ln K_{ps}(T_{ref})+\int_{T_{ref}}^{T^\prime}\frac{\Delta H_{diss}^0} {RT^2}dT$
em que $($equação 15 da referência $[1])$
$\Delta H_{diss}^0(T^\prime) =$
$=\Delta H_{diss}^0(T_{ref})+\int_{T_{ref}}^{T^\prime} \Delta C_p dT$
Os valores de $\Delta C_p$ e $\Delta H_{diss}^0(T_{ref})$ são dados por
$\Delta H_{diss}^0(T_{ref}) = \sum\Delta H_f^0(prod)-\sum\Delta H_f^0(reag) =$
=-252.4-207.4+494.6 = 34.89 kJ/mol= 34890 J/mol
e
$\Delta C_p = \sum\Delta C_p(prod)-\sum\Delta C_p(reag) =$
=-86.6 + 21.8 – 96.4= -161.2 J/mol
As equações acima fornecem o resultado $($equação 16 da referência $[1])$
$\ln K_{ps}(T^\prime)=\ln K_{ps}(T_{ref})$
$-\frac{(\Delta H_{diss}^0(T_{ref})-\Delta C_pT_{ref})}{R}$
$\left(\frac{1}{T^\prime}-\frac{1}{T_{ref}}\right)$
$+\frac{\Delta C_p}{R}(\ln T^\prime-\ln T_{ref})$
Usamos esta equação no lugar da sugerida no Castellan $($equação 11.61$)$. Finalmente
$K_{ps}=e^{\ln K_{ps}}$
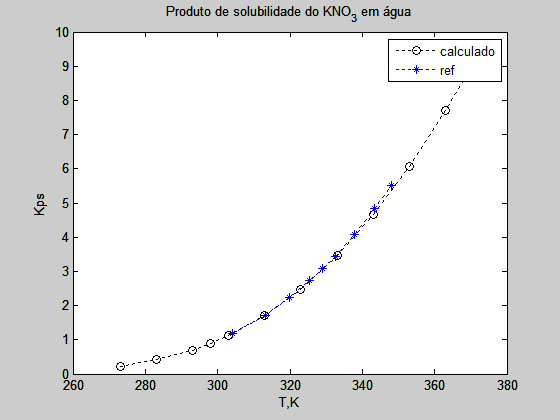
os valores calculados do Kps por este caminho formam comparados com os apresentados na referência $[1]$ Ind. Eng. Chem. Res. 2011, 50, 7019-7026.
$Tart=[304.15; 313.15; 319.95; 325.45; 329.05; 332.45; 337.85; 343.45; 348.15]’;$
$kpsart=[1.17; 1.71; 2.23; 2.73; 3.09; 3.45; 4.09; 4.83; 5.50]’;$
A figura abaixo mostra o resultado da comparação
 Considerando, também é dado por
Considerando, também é dado por
$K_{ps}=a_{K^+}a_{NO_3^-}=\gamma_\pm^2s^2$
tem-se
$\gamma_\pm=\sqrt{\frac{Kps}{s^2}}$
Esta é a expressão para calcular os valores de $\gamma_\pm$ em função da temperatura, a partir dos dados da solubilidade do KNO3. Para a solubilidade do KNO3 usamos os dados abaixo
Handbook pg. 1355
$T=[0; 10; 20; 25; 30; 40; 50; 60; 70; 80; 90; 100];$
Solubilidade em g por 100g de solução*
$s=[12; 17.6; 24.2; 27.7; 31.3; 38.6; 45.7; 52.2; 58; 63; 67.3; 70.8];$
Os valores encontrados para o coeficiente de atividade são apresentados abaixo
T s kps $\gamma_\pm$
273.0000 1.3488 0.2267 0.3530
283.0000 2.1126 0.4099 0.3030
293.0000 3.1578 0.6952 0.2640
298.0000 3.7895 0.8860 0.2484
303.0000 4.5063 1.1141 0.2342
313.0000 6.2180 1.6973 0.2095
323.0000 8.3244 2.4715 0.1889
333.0000 10.8013 3.4555 0.1721
343.0000 13.6588 4.6582 0.1580
353.0000 16.8412 6.0759 0.1464
363.0000 20.3565 7.6927 0.1362
373.0000 23.9820 9.4805 0.1284
*s for convertido para molalidade nos cálculos.
function kno3part1
clear all
close all
%dados tabelas: CRC Handbook pg. 865, 930 e 931
DG025=-283.3-111.3+394.9; DG025=DG025*1000; %0.3kJ/mol
DH025=-252.4-207.4+494.6; DH025=DH025*1000; %34.89kJ/mol
DCp=-86.6+21.8-96.4; %-161.2J/mol
R=8.314;
%CRC Handbook pg. 1355
T=[0 10 20 25 30 40 50 60 70 80 90 100]; T=(T+273)';
%solubilidade em %, Söhnel, O., and Novotny, P., Densities of Aqueous Solutions of Inorganic Substances, Elsevier, Amsterdam, 1985.
s=[12 17.6 24.2 27.7 31.3 38.6 45.7 52.2 58 63 67.3 70.8];
s=s'/100;
%solubilidade em mol/Kg do solvente
s=s*1000./(101.1032*(1-s));
%equação 11.39 do Castellan
kps25=exp(-DG025/(R*298));
%equação 7.75 do Castellan
DH0T=DH025+DCp*(T-298);
%equação (usei no lugar da 11.61 do Castellan)
lnkpsT=log(kps25)-((DH025-DCp*298)/R)*(1./T-1/298)+(DCp/R)*log(T/298);
kpsT1=exp(lnkpsT);
%dados artigo Ind. Eng. Chem. Res. 2011, 50, 7019-7026
Tart=[304.15 313.15 319.95 325.45 329.05 332.45 337.85 343.45 348.15]';
kpsart=[1.17 1.71 2.23 2.73 3.09 3.45 4.09 4.83 5.50]';
%kpsarti = interp1(Tart,kpsart,T);
%plot(T,kpsT1,'b*:',T,kpsarti,'go:',Tart,kpsart,'r*:')
figure
plot(T,kpsT1,'ko:',Tart,kpsart,'b*:')
title('Produto de solubilidade do KNO_3 em água')
legend('calculado','ref')
ylabel('Kps')
xlabel('T,K')
figure
plot(T,s,'ko:',T,sqrt(kpsT1),'b*:')
title('Solubilidade do KNO_3 em água')
legend('exp','\gamma_\pm=1')
ylabel('s, mol/Kg')
xlabel('T,K')
gamapm=sqrt(kpsT1)./s;
[T s kpsT1 gamapm]
end

