Partículas pequenas, tipicamente na faixa de nanômetros (nm) ou micrômetros (µm), suspensas em um fluido, sofrem movimento aleatório devido a colisões com as moléculas do fluido. Esse fenômeno é conhecido como movimento browniano.
Quando um feixe de laser de frequência $\nu$ incide sobre um determinado volume do fluido, as moléculas dentro desse volume iluminado experimentam o campo elétrico incidente. As cargas que as constituem são submetidas a uma força e, consequentemente, aceleradas. De acordo com a teoria clássica do eletromagnetismo, uma carga acelerada emite radiação. O campo elétrico total espalhado, detectado em um dado momento, resulta da superposição dos campos elétricos emitidos por todas as cargas no volume iluminado, dependendo, assim, das posições e dos momentos de todas as partículas no sistema. Devido ao seu movimento térmico, as partículas estão em constante movimento, levando a variações dependentes do tempo na intensidade da luz espalhada em um ângulo $\theta$.
clc; clear; close all;
% Parâmetros do experimento
lambda = 632.8e-9; % Comprimento de onda do laser (m) - Exemplo: HeNe
theta = 90; % ângulo de espalhamento (graus)
n_medium = 1.33; % índice de refração do meio (água)
kb = 1.3806e-23; % constante de Boltzmann (J/K)
T = 298; % temperatura (K)
eta = 0.89e-3; % viscosidade da água (Pa.s)
theta2 = theta*pi/180; % ângulo em radiano
q = (4 * pi * n_medium / lambda) * sin(theta2 / 2); % vetor de onda
% Definição da distribuição de tamanhos de partículas (nm)
R1 = 50*1e-9; % tamanho maior (150 nm)
D1 = kb*T/(6*pi*eta*R1);
gama1 = D1*q^2;
s1 = 20;
R = .001:2:150; R=R*1e-9;
D = kb*T./(6*pi*eta*R);
gama = D*q^2;
P = exp(-((R-R1)*1e9/s1).^2);
P=P/sum(P);
G=P*(kb*T*q^2)./(6*pi*eta*gama.^2);
G=G/sum(G);
%figure
%plot(R,P)
%figure
%plot(gama,G)
tau = logspace(-6, 1, 300);
K = exp(-tau'*gama);
g1 = K*G';
beta =.5;
g2 = 1+beta*g1.^2;
noise_level = 0;
g2_noisy = g2 + noise_level * randn(size(g2));
%data=[tau', g2];
%save('data.txt', 'data', '-ascii');
% Plot do resultado
figure;
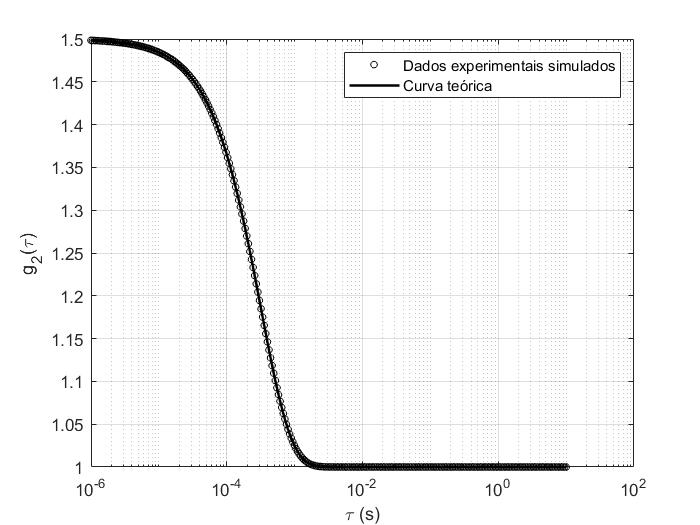
semilogx(tau, g2_noisy, 'ko', 'MarkerSize', 4); hold on;
semilogx(tau, g2, 'k-', 'LineWidth', 1.5);
xlabel('\tau (s)');
ylabel('g_2(\tau)');
%title('Simulação de DLS - Distribuição Bimodal de Tamanhos de Partículas');
legend('Dados experimentais simulados', 'Curva teórica');
grid on;
lam = .05e-4; % Parâmetro de regularização
L = eye(size(K'*K)); % Matriz identidade
g1n=sqrt((g2-1)/beta);
Gn=(K'*K+lam^2*L)\(K'*g1n);
Pr=Gn*kb*T*q^2./(6*pi*eta*R'.^2);
Pr=Pr/sum(Pr);
figure
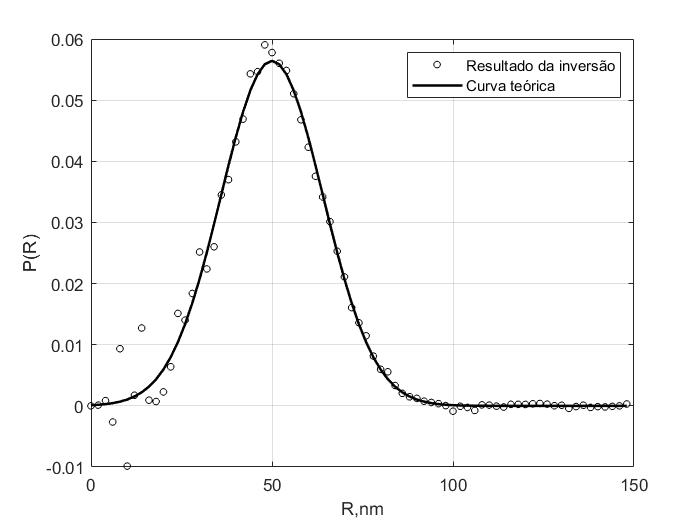
plot(R*1e9,Pr,'ko','MarkerSize',4); hold on;
plot(R*1e9,P,'k-','LineWidth', 1.5);
xlabel('R,nm');
ylabel('P(R)');
%title('Simulação de DLS - Distribuição Bimodal de Tamanhos de Partículas');
legend('Resultado da inversão','Curva teórica');
grid on;