Considere um balde de 20L sob uma torneira aberta, cuja vazão (volume de água que entra no balde por intervalo de tempo) é constante e igual a ϕe = 20 mL/s. Partindo do balde vazio, após o primeiro segundo a quantidade de água no balde é de 20 mL, no segundo seguinte é de 40 mL, mais um segundo temos 60 mL no balde. Pode-se dizer que o balde enche com uma “velocidade” constante de 20 mL/s.
Neste caso, a quantidade de água (volume) no balde em função do tempo t é dado pela expressão
V = ϕe t
Usando esta expressão, pode-se calcular que o balde leva 1000 s para encher.
Agora, considere o mesmo balde (de 20L), com um furo no fundo, sob a mesma torneira. A vazão de água que sai pelo furo é de ϕs = 5 mL/s e a vazão de água que entra no balde é de ϕe = 20 mL/s. Neste caso, o balde enche?
Vejamos, no primeiro segundo a quantidade de água no balde é de 15 mL (entraram 20 mL e saíram 5 mL). Pode-se pensar que no segundo seguinte acontece o mesmo, mas devemos olhar o problema com mais calma!
A vazão de água que entra no balde é constante (depende de abrir ou fechar a torneira, mas se não mexermos nela a vazão é constante, ϕe = 20 mL/s), no entanto o mesmo não acontece com a vazão de água que sai do balde (mesmo que o tamanho do buraco não seja alterado). Conforme o balde enche, a altura de água aumenta no balde e, portanto, a vazão de água que sai aumenta.
Para entender isto, considere um balde cheio de bolas de gude, neste caso: – qual a velocidade de uma bola que sai pelo buraco no fundo? A energia potencial da bola mais alta é dada por
Ep = mgh
Quando esta bola chega no fundo, sua energia potencial é convertida integralmente (~) em cinética, assim,
½ mv2 = mgh
Logo a velocidade da bola quando sai do balde é de
v = √(2gh)
Agora use este resultado para pensar no caso do balde com água.
Sendo assim, a área do buraco, representada por ‘a’, vezes a velocidade calculado anteriormente, v, dá a vazão de água no balde. Obtemos isto a partir de uma simples análise dimensional, assim,
ϕs = av = a√(2gh)
Veja que fazendo a vezes v temos uma grandeza de dimensão volume/tempo. Portanto, a vazão de água que sai pelo buraco depende de h. Neste caso, a vazão de água que sai do balde é proporcional a h.
Agora, a quantidade (volume) de água no balde no tempo t é dada pela expressão seguinte
V = (ϕe – ϕs) t = (ϕe – a√(2gh)) t
considerando que V = 0 em t = 0. Considerando que h = V/A já que V = Ah, onde A é a área da base do balde (supondo um balde aproximadamente cilíndrico), temos que
V = (ϕe – a√(2gV/A)) t
Veja que nesta equação o V aparece em dois lugares.
Devido à dificuldade de isolar V, calculamos t em função de V, logo
t = V/(ϕe – a√(2gV/A))
e fazemos o gráfico Vxt. Então, para ϕe = 700 mL/s = 7 x 10-4 m3/s, a = 3,14 x 10-4 m2 (buraco com diâmetro de 2,0 cm), A =0,0707 m2 (balde com diâmetro de 30 cm) e g = 10 m/s temos o resultado mostrado na Figura 10-1.1.
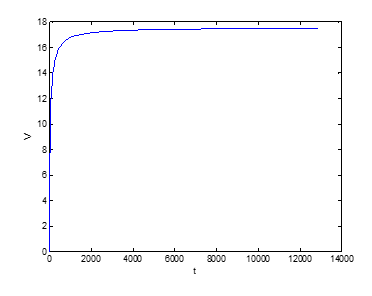
Figura 10-1.1: Volume de água no balde ao longo do tempo. Resultado gerado fazendo a=3.14e-004;A=0.0707;V=0:.1:17.55; V=V/1000; t=V./(70e-5-a*sqrt(2*10*V/A)); plot(t,V*1000);xlabel(‘t’),ylabel(‘V’)
Quando ϕe = ϕs o sistema está em equilíbrio dinâmico e a quantidade de água que entra pela torneira é igual a quantidade de água que sai pelo buraco, a cada segundo. A partir deste instante o volume de água no balde não se altera, apesar do fluxo de água entrando e saindo não parar. Neste caso, temos que ϕe = ϕs e ϕs = a√(2gV/A) então
ϕe = a√(2gVequilíbrio/A)
logo
Vequilíbrio = A(ϕe /a)2/(2g) = 0,0176 m3 = 17,6 L
Este volume é denominado de volume no equilíbrio. Neste caso, não conseguimos encher o balde além deste volume.
O tempo que o sistema leva para entrar em equilíbrio é dado por
trelaxação = Vequilíbrio/(ϕe – a√(2gVequilíbrio/A))
Se substuirmos Vequilíbrio = A(ϕe /a)2/(2g) não equação acima, encontramos
trelaxação = Vequilíbrio/0 → ∞
Portanto, o volume tente assintoticamente ao volume de equilíbrio. Sendo assim, o tempo de relaxação previsto é infinito. Um paradoxo interessante, na prática o balde de fato alcança o volume de equilíbrio!
Em temos práticos considere que estamos tão próximo do equilíbrio quanto desejamos, por exemplo V = 0,99Vequilíbrio. Sendo assim,
t0,99 = V/(ϕe – a√(2gV/A))
t0,99 = 0,99Vequilíbrio/ϕe(1-√0.99)
t0,99 = 0,99Aϕe/(a22g(1-√0.99)) = 4956.8s
i.e. cerca de 82 minutos ou 1 hora e 22 minutos. Interessante, não?

