Considere o sistema formado pelos componentes 1 e 2 $($mistura heterogênea com 2 fases, doravante denominado soma, fase a contém o componente puro 1 e fase b o componente 2 puro$)$, neste caso, a energia livre do sistema é dado por
Gsoma/n = x G1 + (1-x) G2 (1)
Caso, o sistema forme uma única fase $($uma mistura homogênea$)$, existe um decréscimo da energia livre, DG, dado por
$\Delta$G = $\Delta$H – T$\Delta$S (2)
onde, na hipótese de uma mistura ideal,
$\Delta$H = 0
e
$\Delta$S = -R$($xlnx + $($1-x$)$ln $($1-x$)$$)$
Para a mistura ideal $\Delta$S é sempre positivo, i.e. para qualquer x temos $\Delta$S > 0. Como $\Delta$H = 0, então $\Delta$G < 0 para qualquer x e T. Com isto
Gmistura/n = Gsoma/n + $\Delta$G
é sempre menor que Gsoma/n.
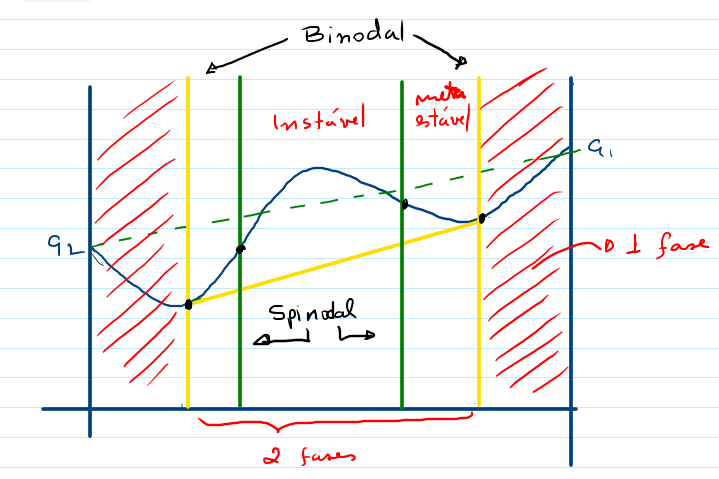
A Figura abaixo mostra a reta que representa a equação $(1)$, como também o resultado obtido pela equação $(2)$.
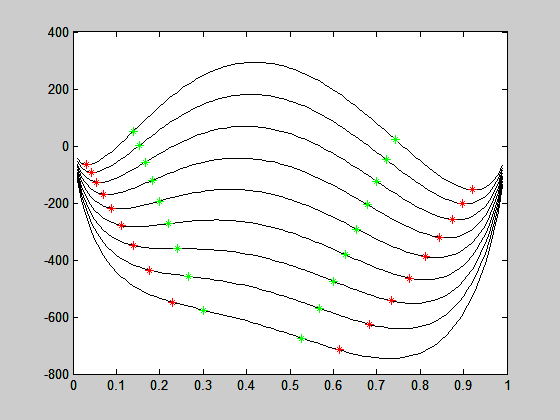
Quando admitimos um valor diferente para DH, tal como
$\Delta H = x(1-x)[A+B(1-2x)]$
Conhecido por modelo de Margules de 2 parâmetros, temos uma curva para Gmistura/n que nem sempre é menor que Gsoma/n. Neste caso, claramente a mistura homogênea dos dois componentes não se forma nestas temperaturas.
Há temperaturas que Gmistura/n é menor que Gsoma/n, no entanto, a concavidade da função Gmistura/n é negativa $($d2G<0$)$ numa faixa de x, indicando uma região de instabilidade. Nesta região, ocorre a separação em duas fases $($alpha e beta$)$ de composições xα e xb. Agora a energia livre deste sistema $($as 2 fases$)$ é dado por
G2fases = nα Gα + nb Gb
Onde
Gα = Gmistura$($xα$)$ e Gb = Gmistura$($xb$)$
Temos também que
nα = (x-xb)n/(nα-xb) e nb =(x-xα)n/(nb-xα)
Neste caso, G2fases$(x)$ é menor Gmistura$(x)$, portanto a formação das duas fases $($uma rica em 1 e outra rica em 2$)$ é mais favorável que a formação de uma mistura homogênea $($uma fase$)$ ou ainda dos dois componentes puros separados. Portanto, queremos resolver
{xα*,xb*} = min{xα,xb} G2fases
para cada temperatura. O resultado representa as composições xα* da fase rica em 2 e xb* da fase rica em 1 na temperatura T. O resultado para diferentes temperaturas é apresentado na figura abaixo:
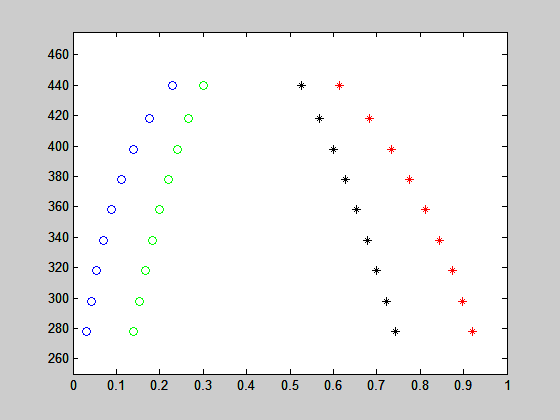
Segue abaixo o programa que gerou as figuras.
function equi
clear all
close all
global A B R
global h
A=7500; B=1000;
R=8.314;
h=1e-3;
T=[278 298 318 338 358 378 398 418 440];
options = optimset('TolFun',1e-5);
x0=[0.1;0.9];
for i=1:length(T)
x(i,:)=fminsearch(@(x) gibbs2(x,T(i)),x0,options);
x0=x(i,:);
end
dados=[T' x]
figure
plot(x(:,1),T,'bo',x(:,2),T,'r*')
axis([0 1 250 475])
save -ascii dados.txt dados
x10=0.2; x20=0.70;
for i=1:length(T)
x1(i)=fzero(@(x) d2gibbs(x,T(i)),x10,options);
G1(i)=gibbs(x1(i),T(i));
x2(i)=fzero(@(x) d2gibbs(x,T(i)),x20,options);
G2(i)=gibbs(x2(i),T(i));
end
dados2=[T' x1' x2']
hold on
plot(x1,T,'go',x2,T,'k*')
for i=1:length(T)
xs=0:.01:1;
DG(:,i)=gibbs(xs,T(i));
end
figure
for i=1:length(T);
plot(xs,DG(:,i),'k-')
hold on
DG1=gibbs(x(i,1),T(i));
plot(x(i,1),DG1,'r*')
plot(x1(i),G1(i),'g*')
DG2=gibbs(x(i,2),T(i));
plot(x(i,2),DG2,'r*')
plot(x2(i),G2(i),'g*')
end
end
function d2G=d2gibbs(x,T)
global h
Gp=gibbs(x+h,T);
G0=gibbs(x,T);
Gm=gibbs(x-h,T);
d2G=(Gm-2*G0+Gp)/h^2;
end
function G=gibbs2(x,T)
Ga=gibbs(x(1),T);
Gb=gibbs(x(2),T);
x1=0.32;
na=(x1-x(2))/(x(1)-x(2));
nb=(x1-x(1))/(x(2)-x(1));
G=na*Ga+nb*Gb;
end
function DG=gibbs(x,T)
global A B R
DH=x.*(1-x).*(A+B*(1-2*x));
DS=-R*(x.*log(x)+(1-x).*log(1-x));
DG=DH-T*DS;
end
Referência: The Behavior of a Pair of Partially Miscible Liquids, S. R. Logan, Journal of Chemical Education Vol. 75 No. 3 March 1998 p. 339.

