Andar do bêbado

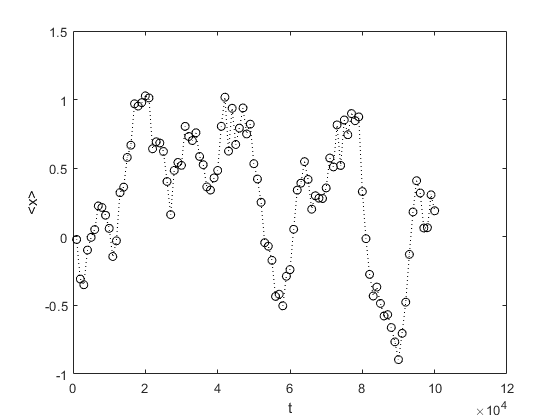
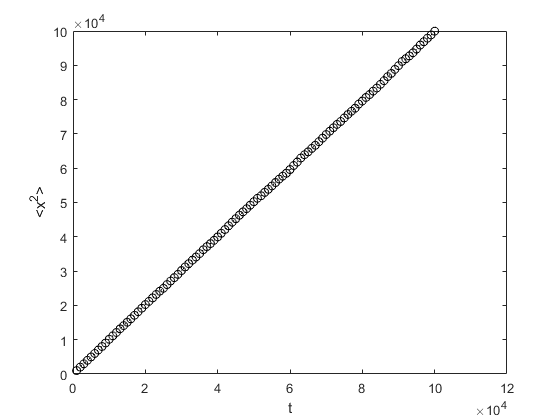
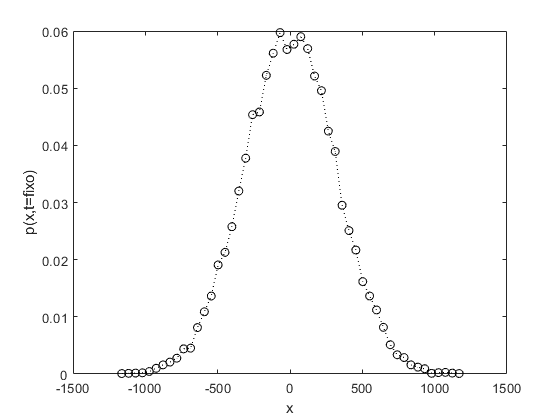
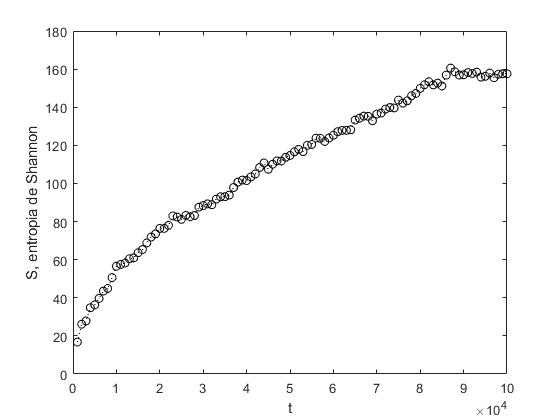
Vamos considerar um indivíduo que se desloca sobre uma reta, a partir da origem, dando passos de comprimento fixo iguais a l=1, para a direita, com probabilidade p=0,5, ou para a esquerda com probabilidade q=1-p=0,5. A implementação do andar do bêbado no MatLab(C) é mostrada abaixo. Veja na figura 2 que o deslocamento quadrático médio é proporcional ao tempo, <x²> ∝ t (difusão não anômala).

clear all
close all
NN=25000;
N=1000:1000:100000;
z=[];
rng(145550)

for j=1:NN
j
x=0; t=0;
for k=1:length(N)
% k
% for j=1:NN
% x=0; t=0;
while t<=N(k)
e=1;
if rand<0.5
e=2;
end
x=x+(-1)^e;
%x=x+(e-1);
t=t+1;
end
q(k)=x; %j=1:N=10000, posição final para o tempo k
r(k)=t; %tempo k=N(k)
end

z(j,:)=q; % posicao final para todos repeticoes tempo k
end

for k=1:length(N)
M(k)=mean(z(:,k)); %media da posicao final no tempo k
J(k)=mean(z(:,k).^2); %media da posicao final quadrática no tempo k
T(k)=r(k); %tempo k=N(k)
end

r1=[T',J']

figure
plot(T,M,'ko:')
xlabel('t')
ylabel('<x>')

figure
plot(T,J,'ko:')
xlabel('t')
ylabel('<x^2>')

for k=1:length(N)
[NX,X(:,k)]=hist(z(:,k),50);
p(:,k)=NX/sum(NX);
zx=find(NX==0);
if length(zx)>0
% 'ERRO'
p(zx,k)=1e-10;
end
end

figure
plot(X(:,end),p(:,end),'ko:')
xlabel('x')
ylabel('p(x,t=fixo)')

for k=1:length(N)
h=abs(diff(X(:,k)));
S(k)=-sum(p(1:end-1,k).*log(p(1:end-1,k)).*h);
end

figure
plot(N,S,'ko:')
[N',S']
xlabel('t')
ylabel('S, entropia de Shannon')

save -ascii r1.txt r1