A maioria dos químicos já ouviu falar da análise de componente principal, PCA. O PCA envolve uma transformação da matriz de dados originas X, de dimensão IxJ cuja as linhas representam amostras e colunas representam variáveis.
| Composto/número de onda (cm-1) | ν1 | ν2 | ν3 | … | νJ |
| C1 | x11 | x12 | x13 | … | x1J |
| C2 | x21 | x22 | x23 | … | x2J |
| C3 | x31 | x32 | x33 | … | x3J |
| … | |||||
| CI | xI1 | xI2 | xI3 | … | xIJ |
O método proposto é influenciado pelo pré-processamento de dados. Neste caso, primeiro centramos as colunas em torno da média
xij=xij-<xj> onde <xj>=∑i=1I xij/I
em seguida fizemos a padronização
xij=xij/sj onde sj=√(∑i=1I (xij-<xj>)2/I)
e, finalmente, X=[xij]. Sendo assim, os elementos xij são as medidas do composto i para a variável j. A transformação sugerida coloca a matriz X na forma
X = TP+E
Na equação acima T é chamada de matriz de scores e possui dimensão IxA, onde A é o número de linhas da matriz P, tal que A≤min(I,J). A matriz P é chamada de matriz loadings e possui dimensão AxJ. O produto TP é uma aproximação de X, sendo o erro representado por E. É importante distinguir a dimensão A do rank da matriz X, k. Abaixo veremos como determinar k e A. O objetivo desta transformação é encontrar um espaço que minimize a covariância dos dados XX’. Uma forma de encontrar este espaço é utilizando a decomposição em valor singular da matriz X,
X = USV’
onde U e V são matrizes ortonormais (neste caso U’=U-1 e V’=V-1) e S é uma matriz diagonal. Os elementos da diagonal da matriz S são chamados de valores singulares, si. As colunas das matrizes U e V, u e v, são chamadas de vetores singulares. O conjunto de valores singulares, em ordem crescente, é chamado de espectro de valores singulares. Dim(X)=[I,J], Dim(U)=[I,I], Dim(S)=[I,J] e Dim(V’)=[J,J]. Neste caso, veja que
XV = USV’V = US
Uma propriedade importante de uma matriz ortonormal é que quando aplicada em um vetor ela preserva a norma original.
YY’ = XV(XV)’ = XVV’X’ = XX’
Logo Y=XV é uma rotação de X em torno da média para o espaço U. Este espaço U é para matriz de covariância de Y um espaço de autovetores ua dos autovalores la=sa2,
YY’ = XV(XV)’ = USSU’ = US2U’
YY’U = S2U
Pode-se observar que a matriz covariância de Y é dada por uma matriz diagonal tendo todos os elementos fora da diagonal iguais a zero sendo, portanto, as variáveis não correlacionadas. A variância é dada pelos elementos da diagonal. Nosso objetivo é encontrar a matriz T tal que X=TP, onde as novas variáveis T são descorrelacionadas e arranjadas em ordem crescente em relação a variância dos dados. Podemos recuperar X a partir de Y usando
X = YV’
Sendo assim P=V’ (loadings) e T=Y=XV=US (scores). O parâmetro k é o rank da matriz X, isto é, número de valores singulares diferentes de zero. A dimensão A≤k, portanto
TA = ∑a=1Atasa
PA = V’(1:A,:)
Assim, Dim(TA)=[I,A] e Dim(PA)=[A,J]. Logo
XA = ∑a=1Ata’pa
ou
xijA = ∑a=1Atiapaj
XA = [xijA] = TAPA.
Neste caso a matriz erro é dada por
E = X–XA
Se A=k, XA=X e E=0. Outras informações usuais são:
Va = 100 la/∑i=1kli = 100 sa2/∑i=1ksi2
∑a=1kVa = 100
RSSA = ∑a=1kla – ∑a=1Ala = ∑a=1ksa2 – ∑a=1Asa2
PRESSA = ∑i=1I∑j=1J(xijA-xij)2
As pessoas gostam de pensar nos t’s como a projeção da X no espaço U, e assim algumas das analogias geométricas podem ser incorporadas.
TABELAS USUAIS:
Tabela 1: la=sa2 | Va | Va acumulado
Tabela 2: la=sa2 | RSSA | PRESSA
GRÁFICOS USUAIS:
Figura 1: t1 (primeira coluna) x composto
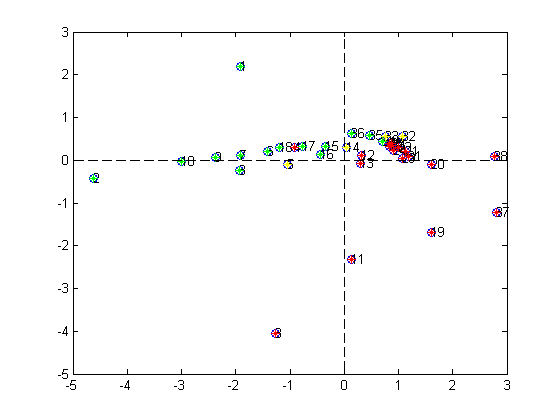
Figura 2: t1 x t2
Figure 3: p1(primeira coluna) x variárel
Figure 4: p1 x p2
Exemplo: Tabela Periódica
function pcaestudotabela
clc
clear all
close all
% Z,RAIO ATOMICO, FIRST IE, SECOND IE, EA, ELETRONEGATIVIDADE
d=[
1 37 1.31 0.00 0.073 2.2
2 32 2.37 5.25 -0.050 5.2
3 134 0.52 7.30 0.060 0.98
4 90 0.90 1.76 0.050 1.57
5 82 0.80 2.43 0.027 2.04
6 77 1.09 2.35 0.122 2.55
7 75 1.40 2.86 -0.007 3.04
8 73 1.31 3.39 0.141 3.44
9 71 1.68 3.37 0.328 3.98
10 69 2.08 3.95 -0.116 4.5
11 154 0.50 4.56 0.053 0.93
12 130 0.74 1.45 -0.039 1.31
13 118 0.58 1.82 0.426 1.61
14 111 0.79 1.58 0.134 1.9
15 106 1.01 1.90 0.072 2.19
16 102 1.00 2.25 0.200 2.58
17 99 1.25 2.30 0.349 3.16
18 97 1.52 2.67 -0.097 3.2
19 196 0.42 3.05 0.048 0.82
20 174 0.59 1.15 -0.029 1
21 144 0.63 1.23 0.018 1.36
22 136 0.66 1.31 0.008 1.54
23 125 0.65 1.41 0.051 1.63
24 127 0.65 1.59 0.064 1.66
25 124 0.72 1.51 0.000 1.55
26 125 0.76 1.56 0.016 1.83
27 126 0.76 1.65 0.064 1.88
28 121 0.74 1.75 0.115 1.91
29 138 0.75 1.96 0.119 1.9
30 131 0.91 1.73 -0.050 1.65
31 126 0.58 1.98 0.029 1.81
32 122 0.76 1.54 0.116 2.01
33 119 0.95 1.80 0.078 2.18
34 116 0.94 2.05 0.195 2.55
35 114 1.14 2.10 0.325 2.96
36 110 1.35 2.35 -0.097 2.9
37 211 0.4 2.6 0.047 0.82
38 192 0.55 1.06 -0.029 0.95];
l=d(:,1);
x1=d(:,1);
x2=d(:,2);
x3=d(:,3);
x4=d(:,4);
x=[x1 x2 x3 x4];
figure
plot(l,x1,'k',l,x2,'b',l,x3,'r',l,x4,'g')
[N,M]=size(x);
xm=mean(x); sm=std(x);
for m=1:M
x(:,m)=(x(:,m)-xm(m))./sm(m);
end
[U,S,V]=svd(x); s=diag(S); VT=V'; A=rank(x);
T=U(:,1:A)*S(1:A,1:A);
P=VT(1:A,:);
for i=1:N
for j=1:M
xe(i,j)=sum(T(i,:)*P(:,j));
end
end
e=x-xe
for i=1:A
Va(i)=100*s(i)^2/sum(s.^2);
Vaa(i)=sum(Va(1:i));
end
disp('Tabela 1')
[s.^2 Va' Vaa']
for i=1:A
RSSA(i)=sum(s.^2)-sum(s(1:i).^2);
T=U(:,1:i)*S(1:i,1:i);
P=VT(1:i,:);
xi=T*P;
PRESSA(i)=sum(sum((xi-x).^2));
end
disp('Tabela 2')
[s.^2 RSSA' PRESSA']
figure(1)
plot(l,T(:,1),'k',l,T(:,2),'b')
figure(2)
plot(T(:,1),T(:,2),'bo')
hold on
for i=1:N
texto=num2str(l(i));
text(T(i,1),T(i,2),texto);
end
pos1=[3 4 11 12 13 19 20 21 22 23 24 25 26 27 28 29 30 31 37 38];
pos2=[1 2 6 7 8 9 10 15 16 17 18 34 35 36];
pos3=[5 14 32 33];
plot(T(pos1,1),T(pos1,2),'r*')
plot(T(pos2,1),T(pos2,2),'g*')
plot(T(pos3,1),T(pos3,2),'Y*')
plot([0 0],[-5 3],'k--')
plot([3 -5],[0 0],'k--')
figure(3)
plot(1:M,P(:,1),'k',1:M,P(:,2),'b')
figure(4)
plot(P(:,1),P(:,2),'bo')

