Considere a equação parabólica
$\frac{\partial f(x,t)}{\partial t}=k\frac{\partial^2 f(x,t)}{\partial x^2},$
que é a forma da equação de condução de calor. Observe que $f$ é uma função das variáveis $x$ e $t$ e que na equação aparece derivadas em relação a estas duas variáveis. Usando diferença finita para a derivada temporal e uma média entre $t+\Delta t$ e $t$ no cálculo de $f_{xx}$, tem-se
$f_{xx}(x,t)=\frac{f(x+\Delta x,t)-2f(x,t)+f(x-\Delta x,t)}{\Delta x^2}.$
e
$f_{xx}(x,t+\Delta t)=\frac{f(x+\Delta x,t+\Delta t)-2f(x,t+\Delta t)+f(x-\Delta x,t+\Delta t)}{\Delta x^2},$
assim,
$\frac{f(x,t+\Delta t)-f(x,t)}{\Delta t}=\\ k\frac{f(x+\Delta x,t+\Delta t)-2f(x,t+\Delta t)+f(x-\Delta x,t+\Delta t)+f(x+\Delta x,t)-2f(x,t)+f(x-\Delta x,t)}{2\Delta x^2}$
Agora, podemos organizar isto como
$f(x,t+\Delta t)-r[f(x+\Delta x,t+\Delta t)-2f(x,t+\Delta t)+f(x-\Delta x,t+\Delta t)]=\\f(x,t)+r[f(x+\Delta x,t)-2f(x,t)+f(x-\Delta x,t)]$
e, finalmente escrever,
$-rf(x+\Delta x,t+\Delta t)+(1+2r)f(x,t+\Delta t)-rf(x-\Delta x,t+\Delta t)=\\rf(x+\Delta x,t)(1-2r)f(x,t)+rf(x-\Delta x,t)$
onde $r=k\Delta t/(2\Delta x^2)$. temos neste caso um sistema de equações, uma equação para cada valor de $x$.
O sistema de equações de Crank-Nicolson pode ser colocado na forma matricial
$({\bf I}-r{\bf D2}){\bf f}(t+\Delta t)=({\bf I}+r{\bf D2}){\bf f}(t)$
onde ${\bf D2}$ é o operador matricial da derivada segunda,
${\bf D2}=\left[\begin{array}{ccccc}
1 & -2 & 1 & & \\
1 & -2 & 1& &\\ & 1& -2& 1&\\&\ddots &\ddots &\ddots & \\& 1& -2& 1&\\& & -1 & 2 & -1\\
& & 1& -2&1\\
\end{array}\right]$
Assim, a solução no tempo $t+\Delta t$ é dado por
${\bf f}(t+\Delta t)=({\bf I}-r{\bf D2})^{-1}({\bf I}+r{\bf D2}){\bf f}(t)$
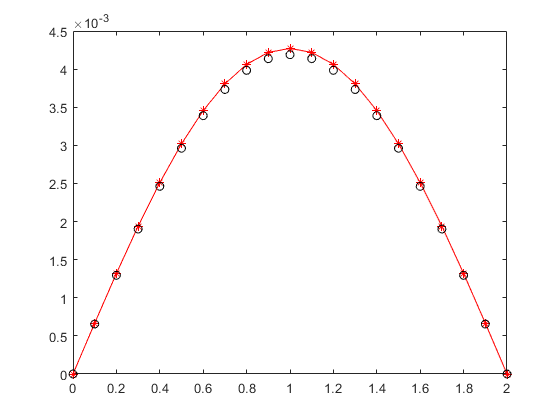
A implementação do método no MatLab (c) é dada abaixo para solução do exercício 5, p. 426, do Boyce 3 edição.
% exercício 5, p.426, [Boyce]
k=1/4; L=2; tmax=10;
dx=.1; r=.1;
dt=r*2*dx^2/k; x=0:dx:L; I=length(x); J=tmax/dt;
%condição inicial
f=2*sin(pi*x/2)-sin(pi*x)+4*sin(2*pi*x); f=f';
N=I;
D2=diag(ones([N-1,1]),-1)-2*diag(ones([N,1]),0)+diag(ones([N-1],1),1);
D2(1,1)=1;D2(1,2)=-2;D2(1,3)=1;D2(N,N-2)=1;D2(N,N-1)=-2;D2(N,N)=1;
A1=(eye(N)-r*D2); A2=(eye(N)+r*D2); A=inv(A1)*A2;
for j=1:J-1
f=A*f;
%condição de contorno
f(1)=0;
f(I)=0;
end
u=2*exp(-pi^2*tmax/16)*sin(pi*x/2)-exp(-pi^2*tmax/4)*sin(pi*x)+...
4*exp(-pi^2*tmax)*sin(2*pi*x);
plot(x,f,'r-*',x,u,'ko')