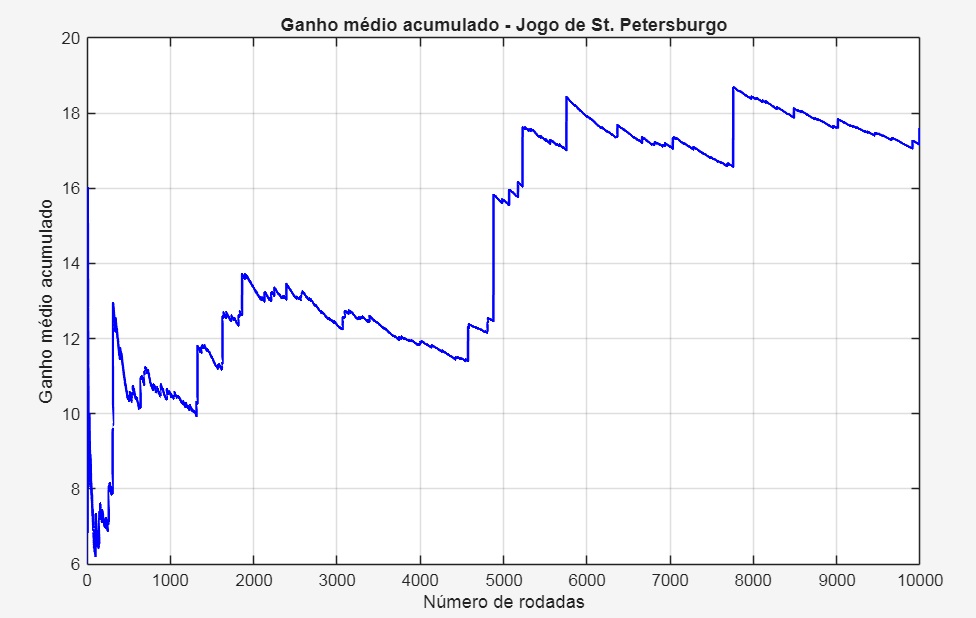
Considere o jodo de moeda, com a seguinte regra:para cada rodada do jogo, lance a moeda até sair cara. Seja n o número de lançamentos realizados até que uma cara apareça. Por exemplo, se a sequência for Coroa, Coroa, Cara (CCc), então n=3. Então, a quantia de dinheiro que você recebe é $2^n$. Portanto, o ganho para a sequência CCc é $2^3=8$ Reais. Este jogo foi introduzido pelo matemático suíço Daniel Bernoulli em meados do século XVIII. Às vezes, ele é referido como o paradoxo de St. Petersburgo ou loteria de St. Petersburgo. A página da Wikipedia sobre o paradoxo de St. Petersburgo é bastante clara e informativa. Suponha que você tivesse a oportunidade de jogar este jogo, mas precisasse pagar algum valor antecipadamente para isso. Quanto você pagaria? Seria vantajoso pagar 5,00 Reais pela chance de jogar este jogo? Qual é o ganho médio do jogo de St. Petersburgo? O que acontece se jogarmos este jogo muitas e muitas vezes? O resultado é, de certa forma, intrigante.Quando parece que o ganho médio estaria se aproximando de uma média, a média dispara de forma abrupta. É como se estivéssemos tentando determinar a altura média dos estudantes em um campus universitário e, raramente, encontrássemos um estudante com 30 ou 300 metros de altura.Portanto, precisamos de mais dados! Mas novamente quando parece que o ganho médio estaria se aproximando de uma média, a média dispara de forma abrupta. Exemplos de fenômenos geralmente considerados semelhantes ao jogo de St. Petersburgo incluem a frequência e severidade de terremotos, a popularidade de sites, os tamanhos de corporações, as populações de cidades e a frequência de uso de palavras. Estes fenômenos seguem uma distribuição com lei de potência, caracterizada por uma cauda longa.