Estamos atualmente sendo bombardeados com a informação de uma curva que deve ser achatada, mas que curva é esta? Temos visto nos últimos dias uma aumento rápido do número de casos do covid-19, é possível prever a evolução do número de casos no brasil? Estas são algumas das questões pertinentes ao momento que vivemos hoje, e que embora fora do contexto da Química, utilizam as mesma ferramentas e ideias necessárias para estudar a velocidade que uma reação química ocorre.
Suponha que N é o número de casos de Covid-19 no brasil, este número de casos aumenta a cada dia, portanto podemos dizer que N é uma função do tempo t, i.e. N=f(t) ou simplesmente N(t). A questão fundamental hoje é saber que função é esta, como é o comportamento de N em função de t?
Uma parte da Epidemiologia, ciência que estuda as doenças no cenário social, é dedicada a construção de modelos capazes de prever este comportamento. Este modelos são muito similares aos que discutimos no caso de reações químicas, onde estamos interessados em descobrir como a quantidade de um reagente muda ao longo do tempo.
O que mais se tem escutado é que o número de caso vem crescendo geometricamente ou exponencialmente. Mas o que significa isto? Uma progressão geométrica é uma sequência numérica na qual cada termo, a partir do segundo, é igual ao produto do termo anterior por uma constante, chamada de razão da progressão geométrica. Vamos supor que o número de casos dobre a cada dia, então iniciando com 2 teremos 4, 8, 16, 32. A razão desta progressão é 2. Podemos escrever isto da seguinte forma
N1 = 2 N0
então
N2 = 2 N1 = 2 2 N0
Podemos também escrever isto da seguinte forma
N2 = 22 N0
Repetindo o processo n vezes temos
Nn = 2n N0
onde n=1,2,3 … Veja que quanto mais afastado do início maior o n, n é como um tempo, então reescreva a equação como
N(t) = 2t N(0)
Agora imagine que no lugar do 2 temos eln2 que é igual a 2. Logo
N(t)= N(0) e(ln2)t = N(0) ekt
Portanto, se o crescimento dos números tiver uma razão igual a 2 o crescimento é exponencial com taxa ln2. Neste caso, a função que dá o número de casos em relação ao tempo é
N(t) = N(0) ekt
Lembra de da disciplina de cálculo que esta função tem uma característica interessante. A derivada de uma exponencial é a própria exponencial, então para uma função deste tipo satisfaz a relação
dN(t)/dt = kN(t)
Portanto, esta é a equação diferencial que governa a dinâmica de um processo exponencial.
No entanto claramente temos um problema com uso da equação acima para descrever o número de casos. De acordo com este modelo o número de casos cresce, cresce, cresce, só cresce! E sabemos que não é assim, chega num momento que o número de casos deve estabilizar.
Para descrever de maneira mais apropriada a dinâmica de uma epidemia temos o modelo SIR descrito pelas equações
dS/dt=-b IS/N
dI/dt= b IS/N – g I
dR/dt= g I
onde t é o tempo, S(t) é o número de pessoas suscetíveis no tempo t, I(t) é o número de pessoas infectadas no tempo t e R(t) é o número de pessoas retiradas (que ganharam imunidade por ter tido a doença ou mortas) no tempo t. Os parâmetros b e g representam a taxa de contágio e a taxa de recuperados no período, respectivamente. Neste modelo a população total N=S+I+R é constante.
I(t) = total de casos(t)-R(t)
R(t) = recuperados(t)+mortos(t)
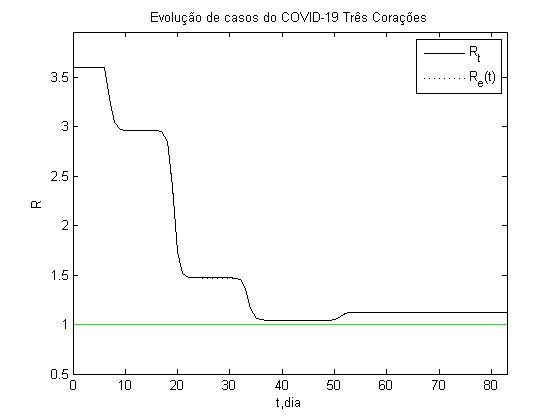
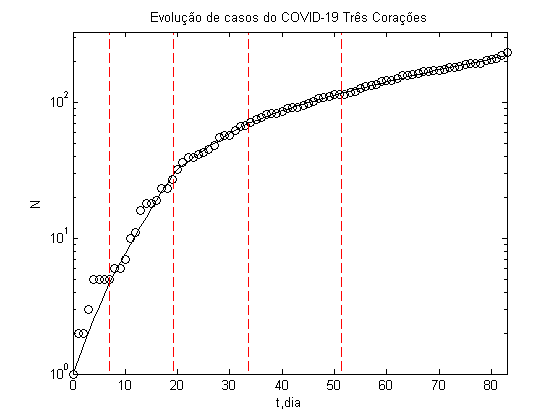
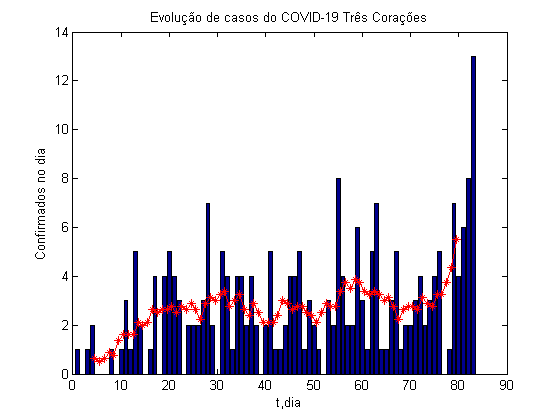
Abaixo mostro o resultado deste modelo e a comparação com os dados de três Corações até a data de 7 de julho. Os dados foram retirados dos Boletins diários da Prefeitura Municipal de Três Corações. Este resultado foi obtido incluindo uma dependência temporal para o parâmetro b, assim b foi trocado por b(t) nas equações acima. A Reprodutibilidade Basal (R0) é dada por b/g, no nosso caso Rt=b(t)/g. O Re, reprodutividade basal equivalente (ou número efetivo de reprodução), é definido por Re=RtS(t)/S(0). Teremos o controle da doença quando Re for menor do que 1, neste caso a doença tende a desaparecer da população. Um indicador acima deste valor indica a necessidade de manutenção de medidas de isolamento. O valores apresentados aqui devem ser considerados apenas como indicativo de tendência da evolução da doença. O dia 0 é o dia do primeiro caso de COVID-19 confirmado na cidade. O primeiro gráfico apresenta a Reprodutibilidade Basal equivalente (Re) em função do tempo (t,dia), o segundo gráfico apresenta o logaritmo do número de casos confirmados (log N) em função do tempo (t,dia) e o terceiro gráfico número de casos confirmados no dia em função do tempo (t,dia), juntamente com a média móvel – estrelas – (janela de 15 dias). O cálculos foram implementados no MatLab(c).