Exemplo para autovalores reais distintos
– autovalores positivos
Considere o sistema
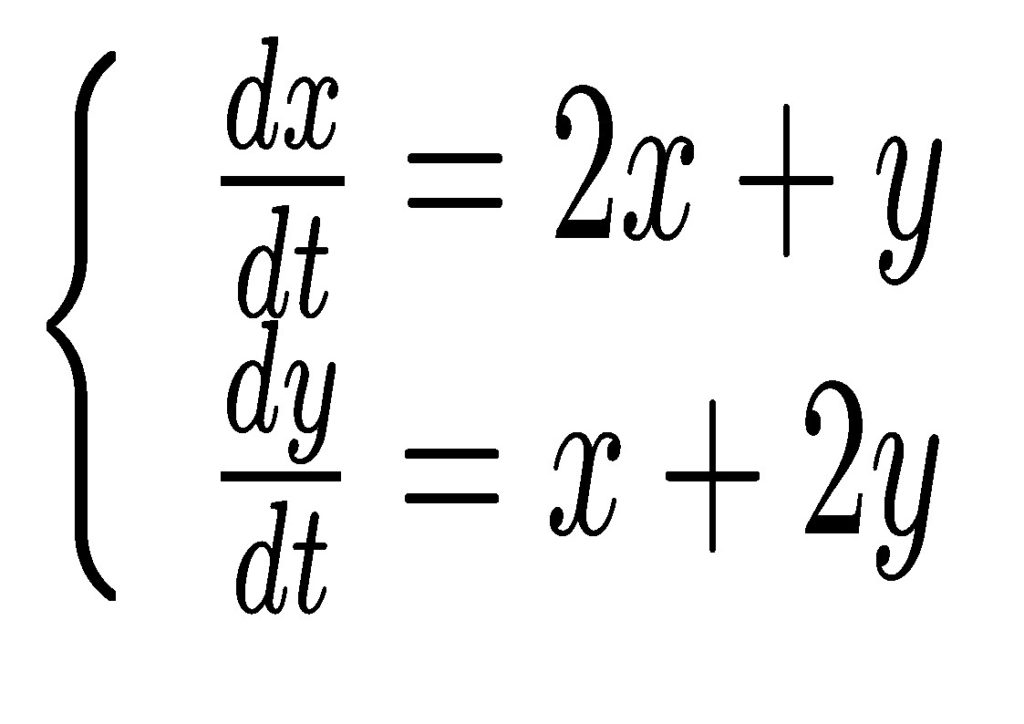
A matriz correspondente ao sistema tem o autovetor (1,-1) associado ao autovalor 1 e o autovetor (1,1) associado ao autovalor 3. Portanto solução geral é dada por
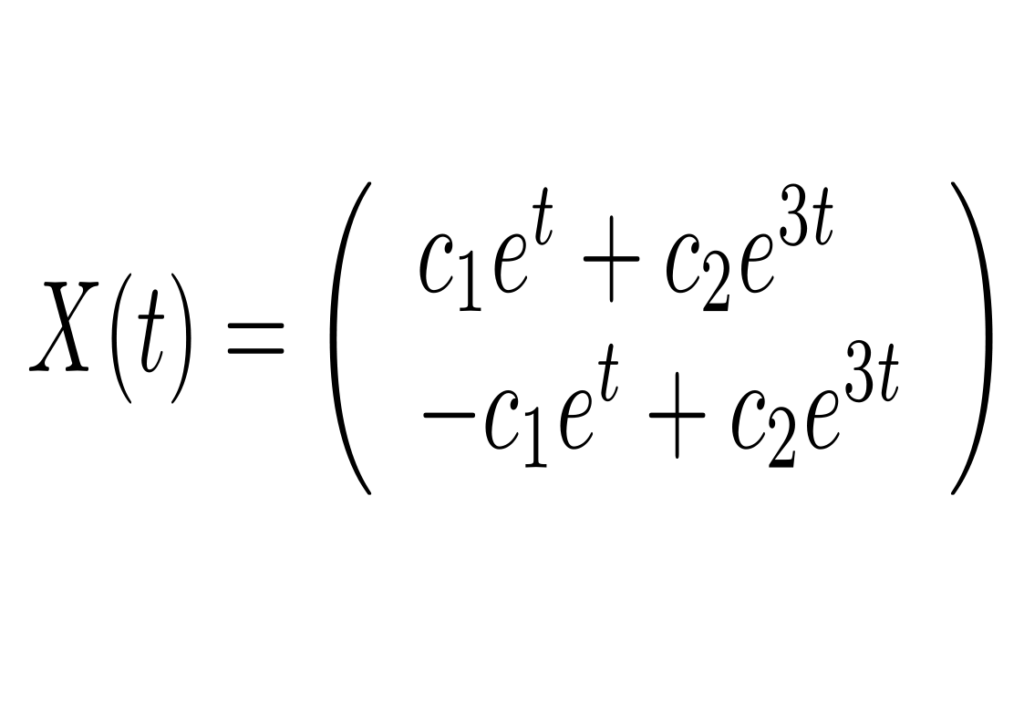
Nos casos em que c1=0 ou c2=0 temos
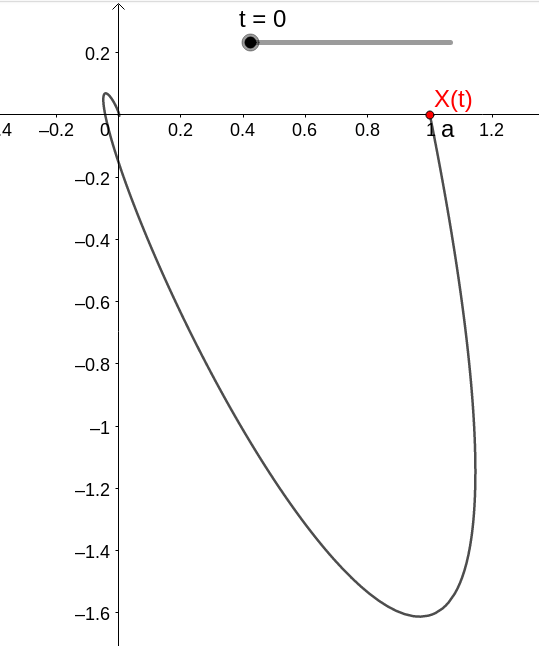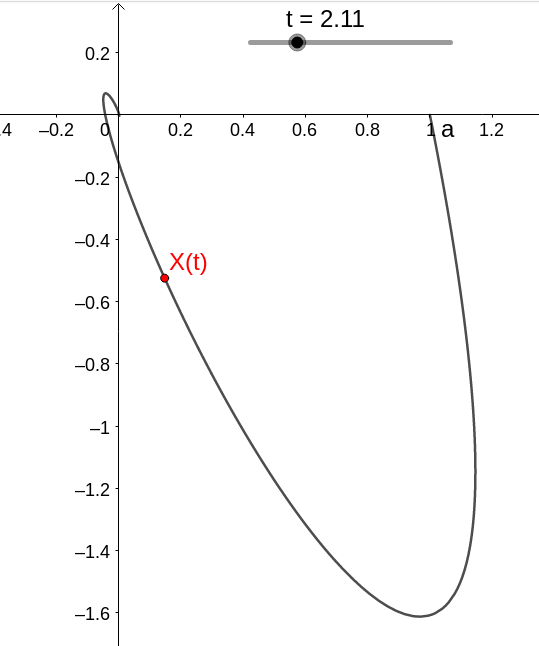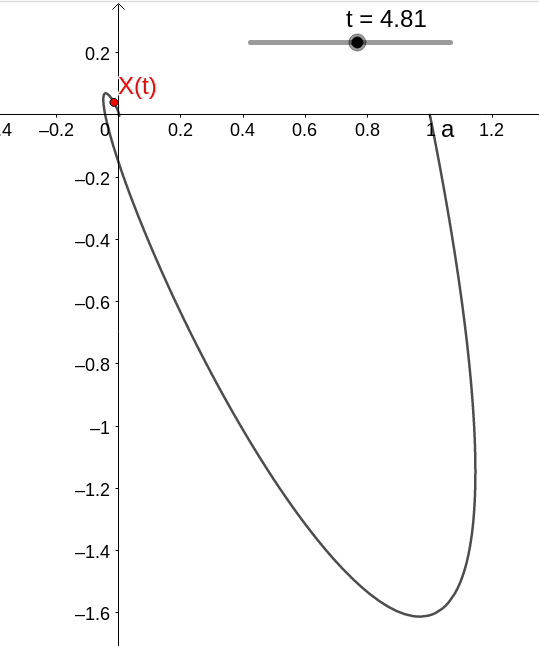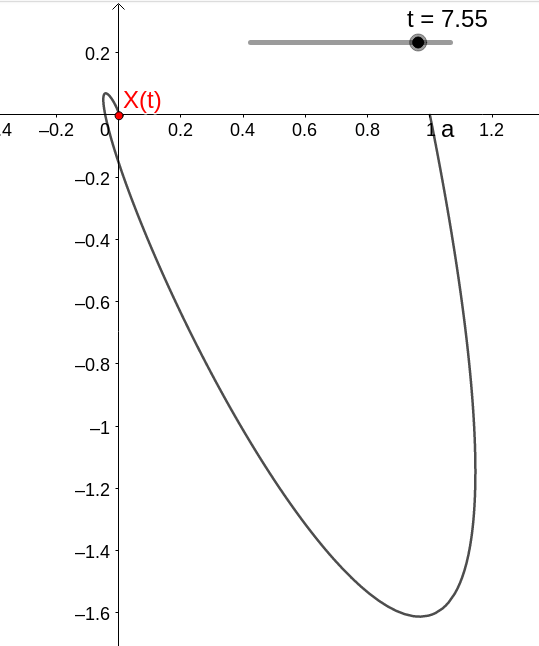
Para condição inicial X(0)=(1,0), temos a solução dada por
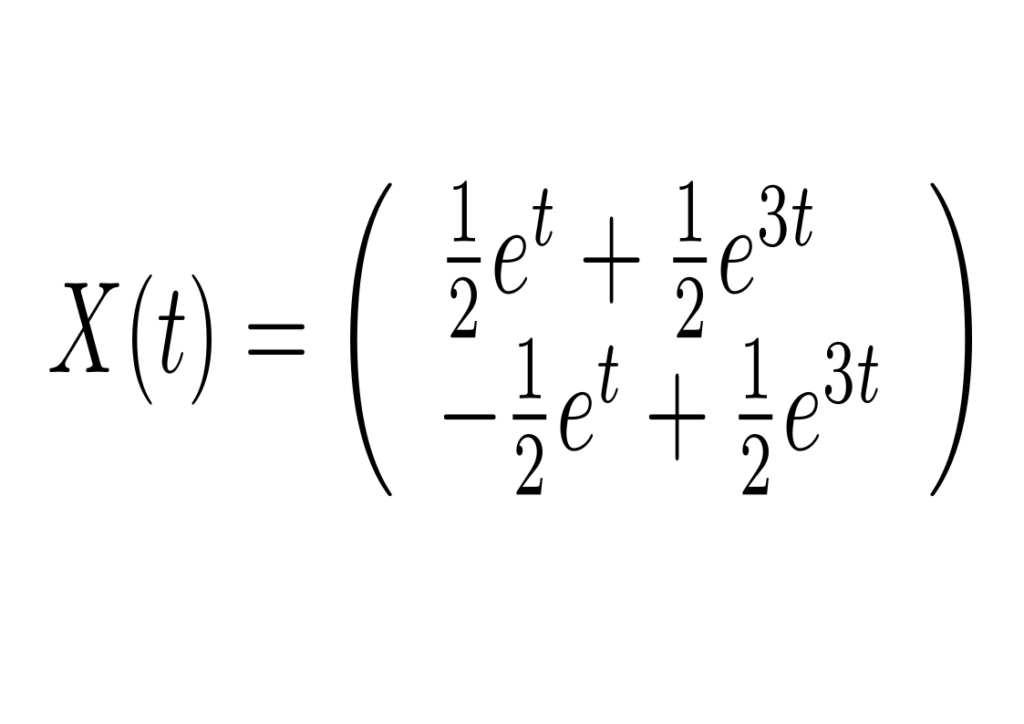
com dinâmica dada por
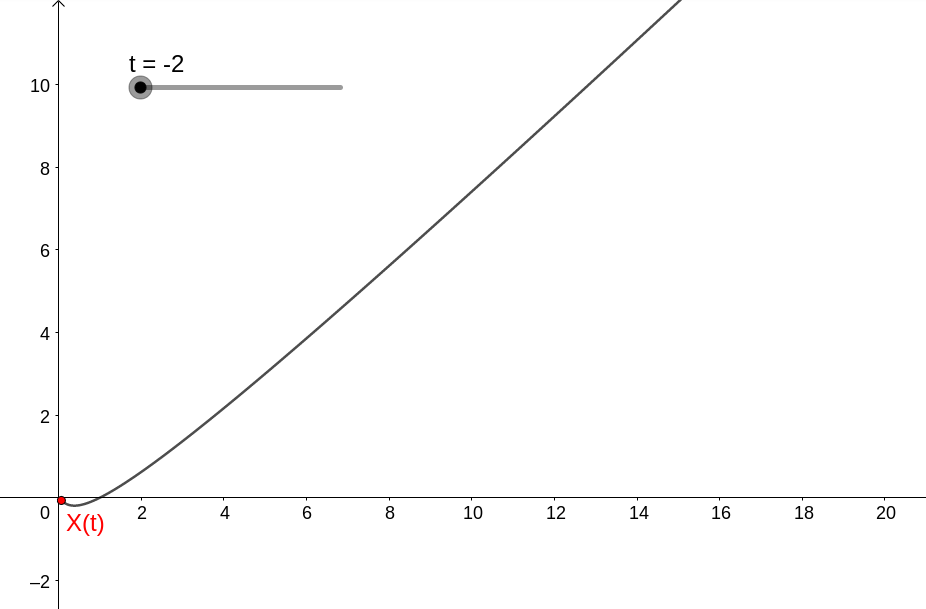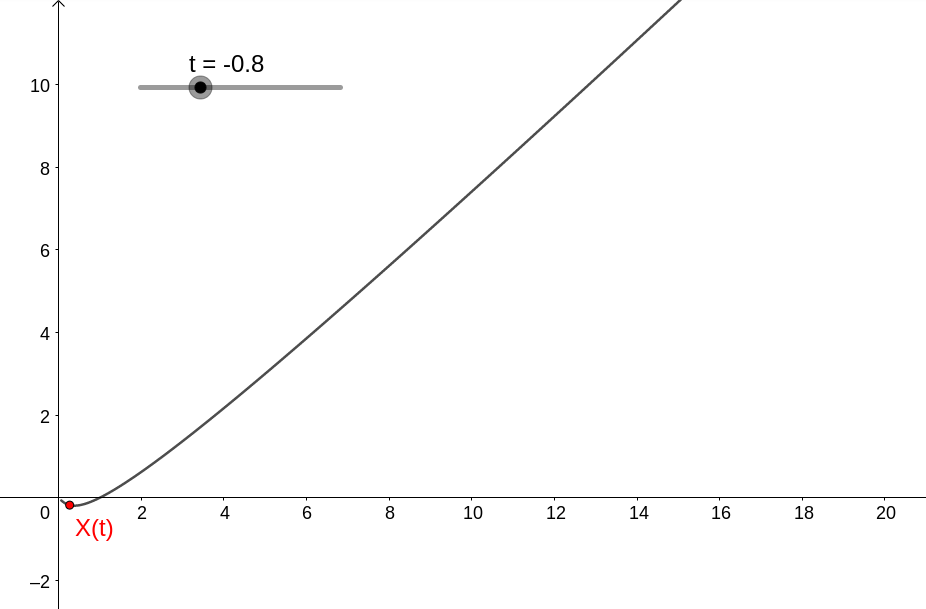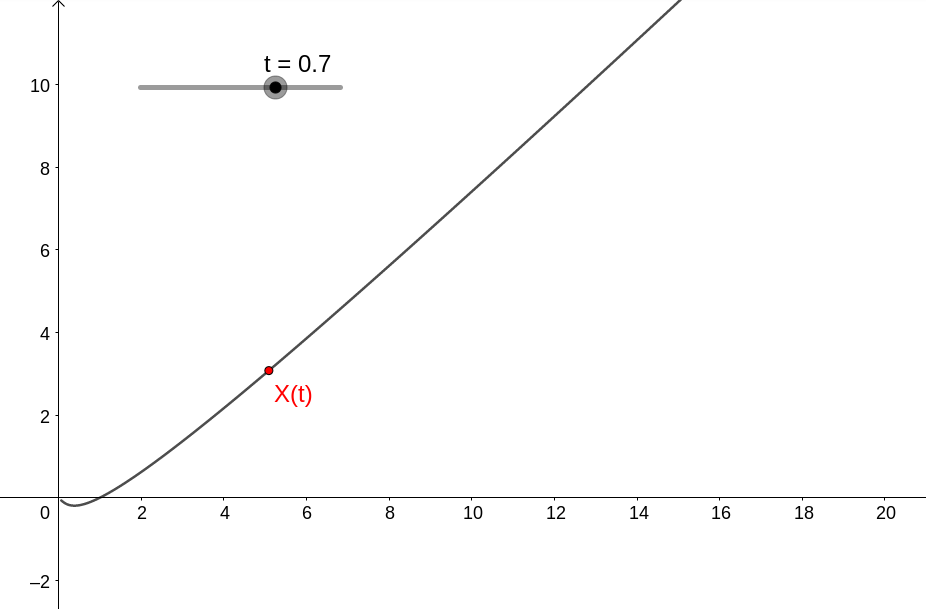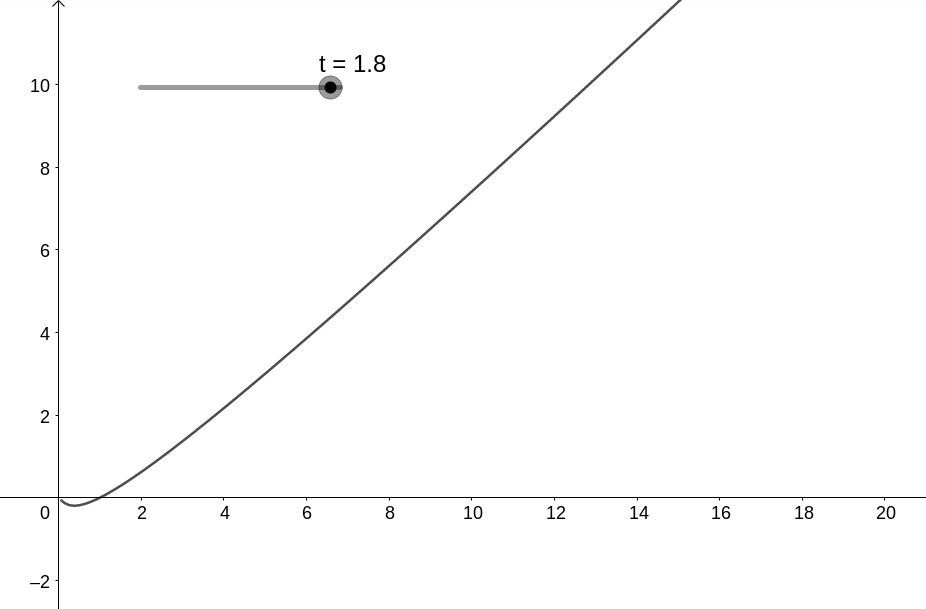
ou seja, no caso temos que (0,0) é instável.
– autovalores negativos
Considere o sistema
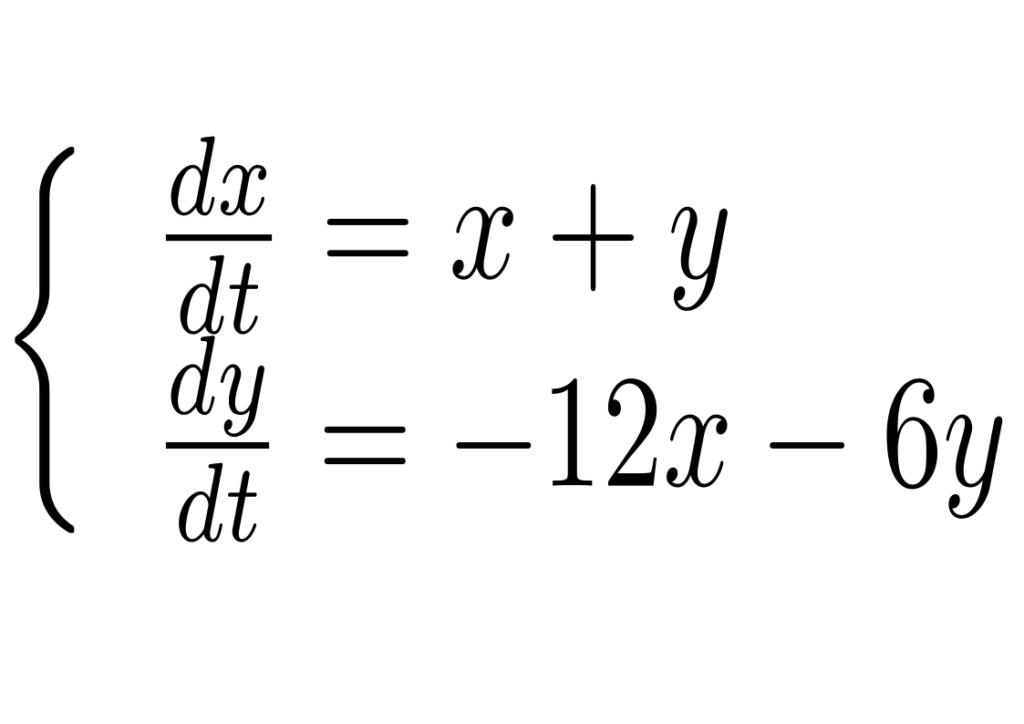
A matriz correspondente ao sistema tem o autovetor (1,-3) associado ao autovalor -2 e o autovetor (1,-4) associado ao autovalor -3. Portanto solução geral é dada por
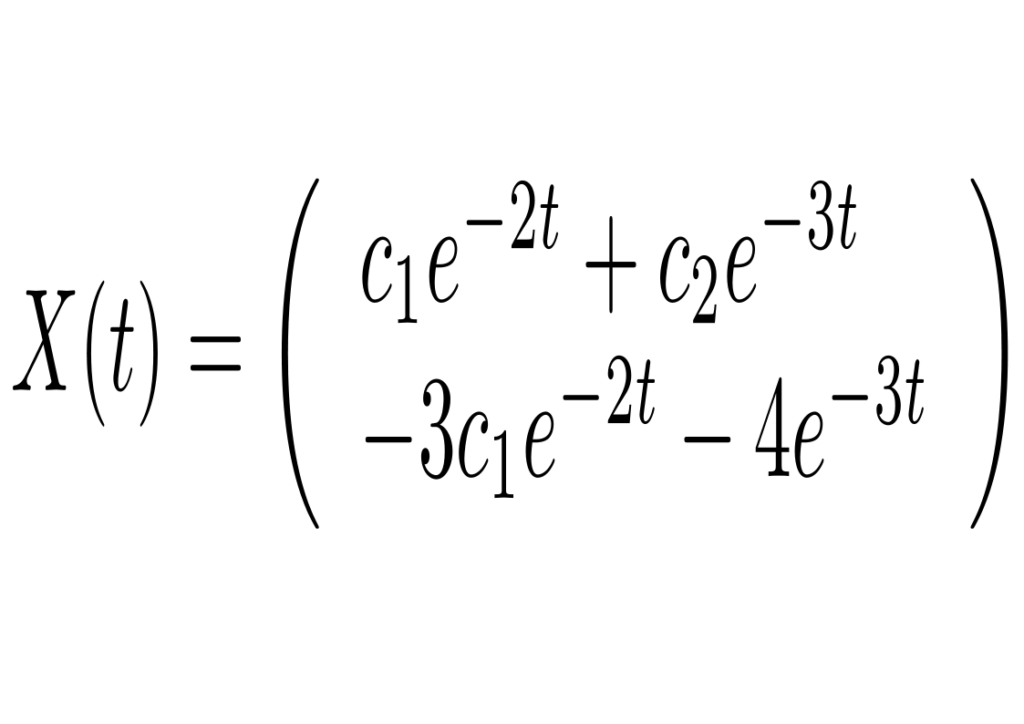
Nos casos em que c1=0 ou c2=0 temos
com a condição inicial X(0)=(1,0) temos
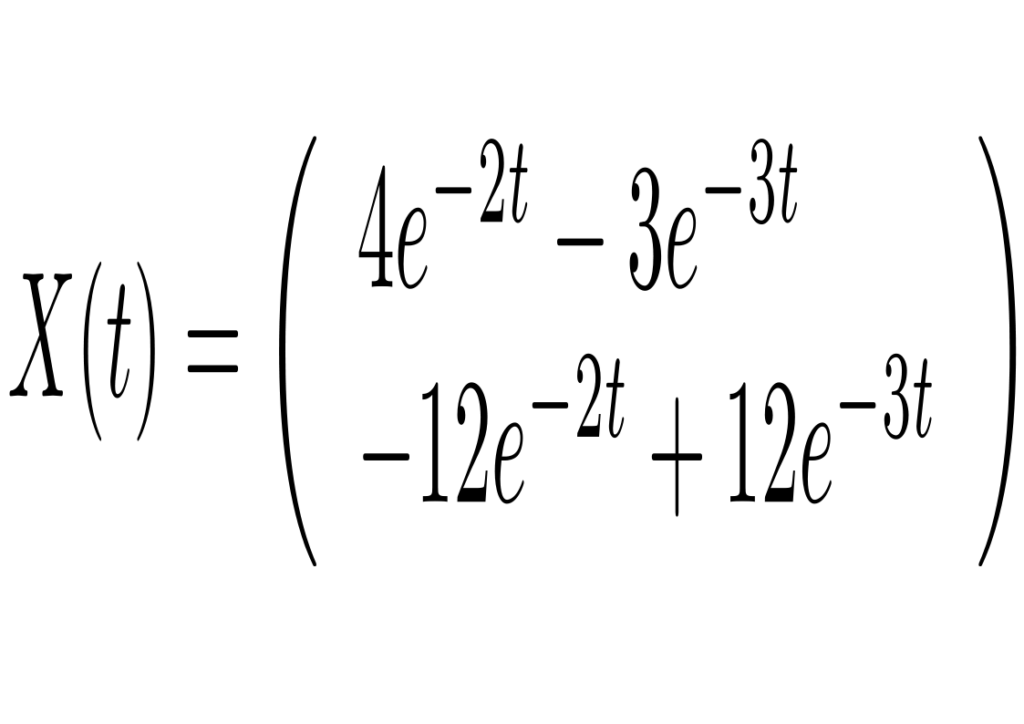
com a dinâmica dada por
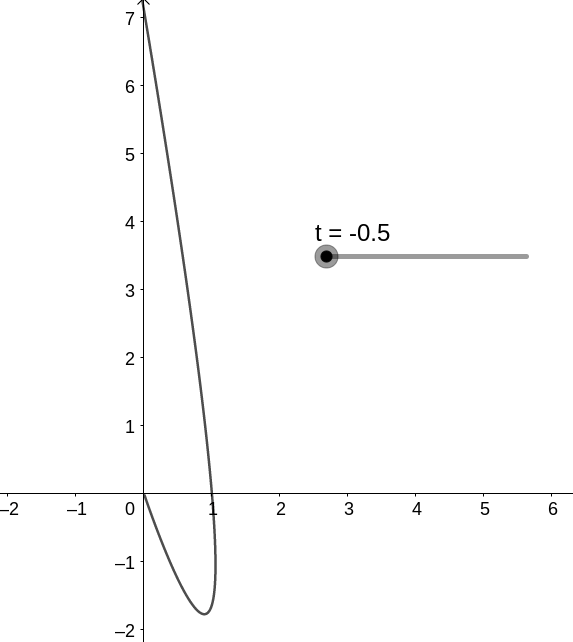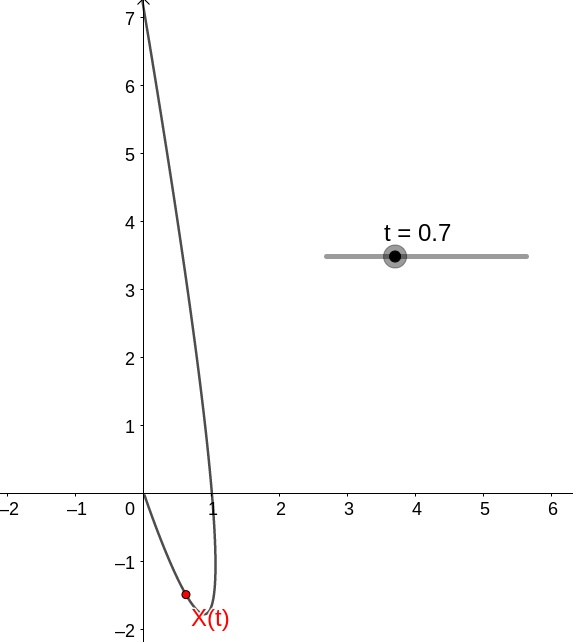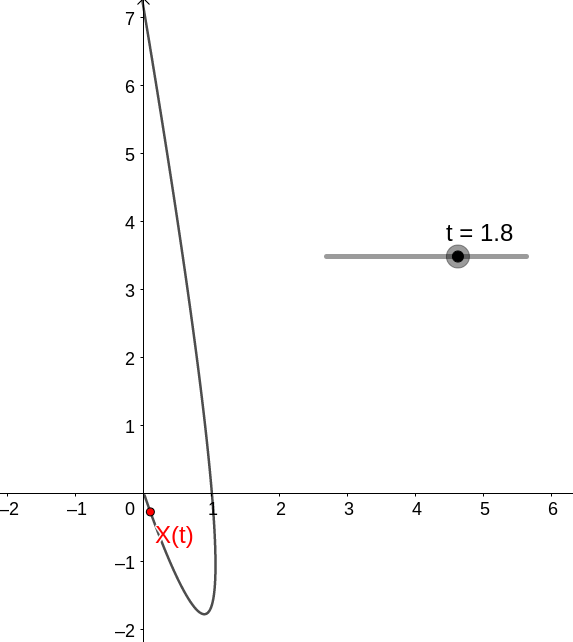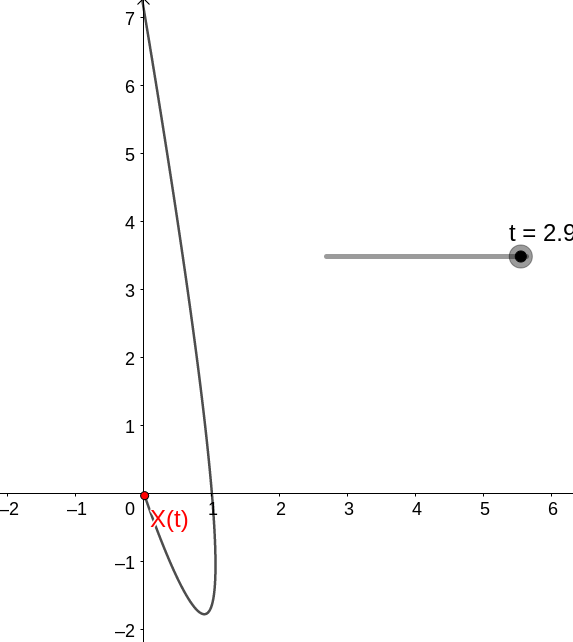
ou seja, no caso temos que (0,0) é estável.
Exemplo para autovalores repetidos
Considere o sistema
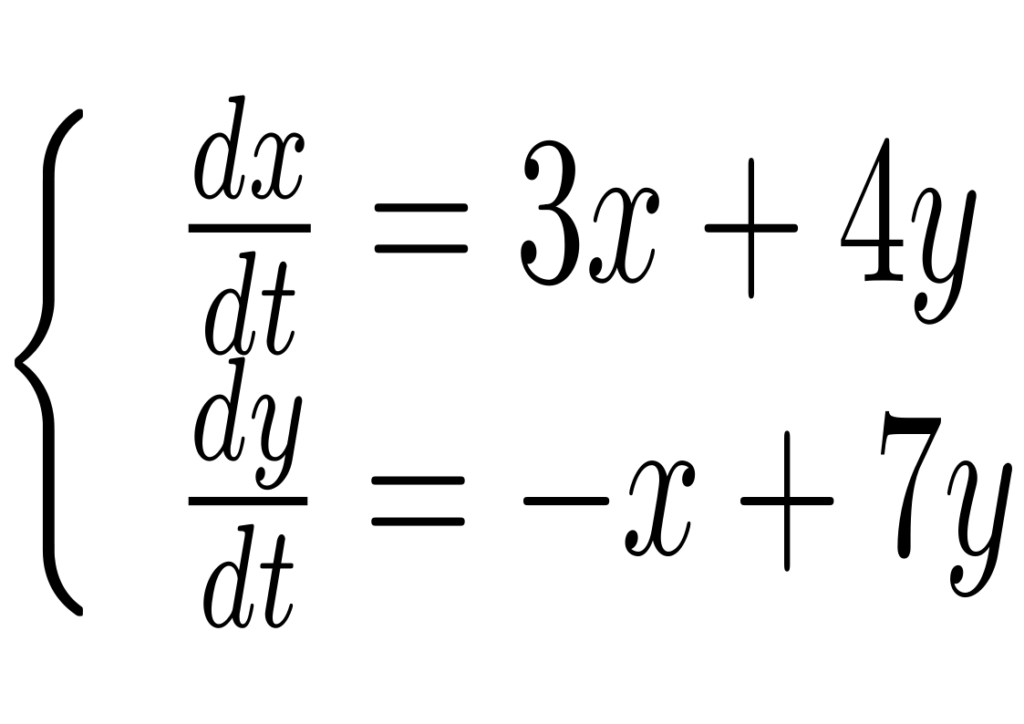
A matriz correspondente ao sistema tem o autovetores linearmente independentes (2,1) e (2,1/2) ambos associados ao autovalor 5. Portanto solução geral é dada por
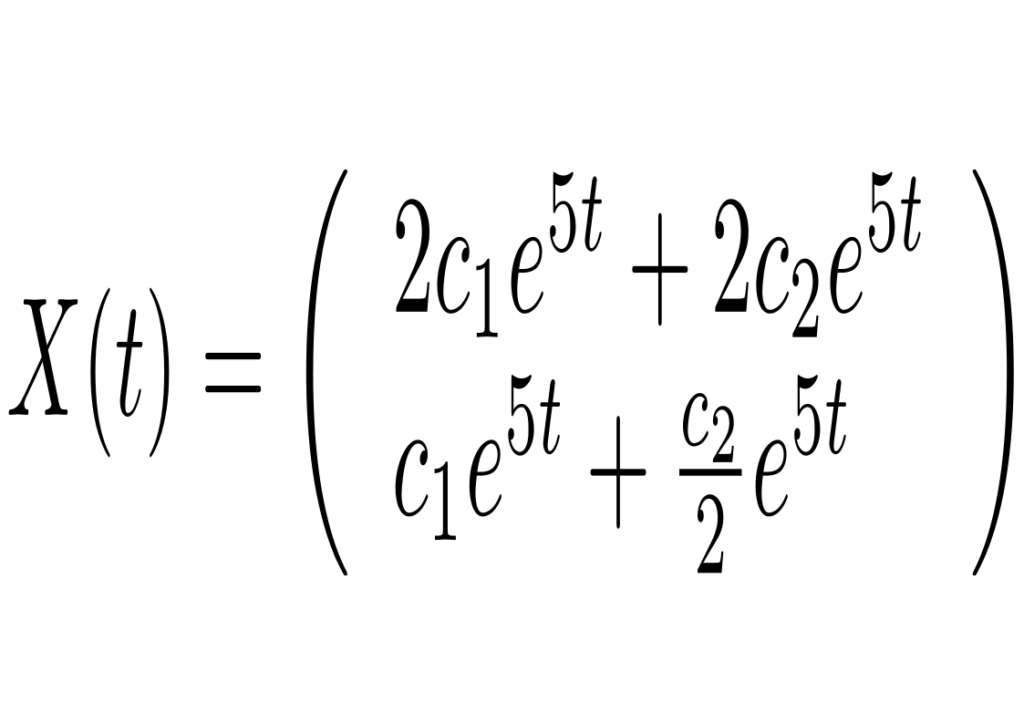
com c1=0 ou c2=0 obtém-se o seguinte gráfico de instabilidade
Com a condição inicial X(0)=(1,0), temos que
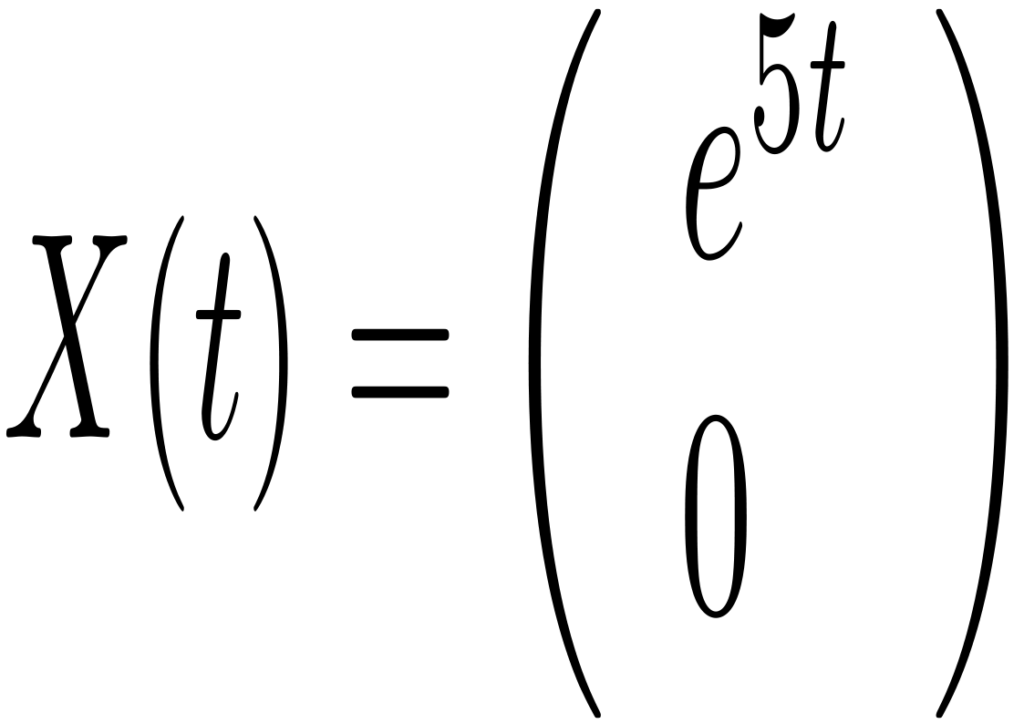
com a dinâmica
ou seja, o ponto (0,0) é instável.
Exemplo de estabilidade para autovalores complexos
Considere o sistema
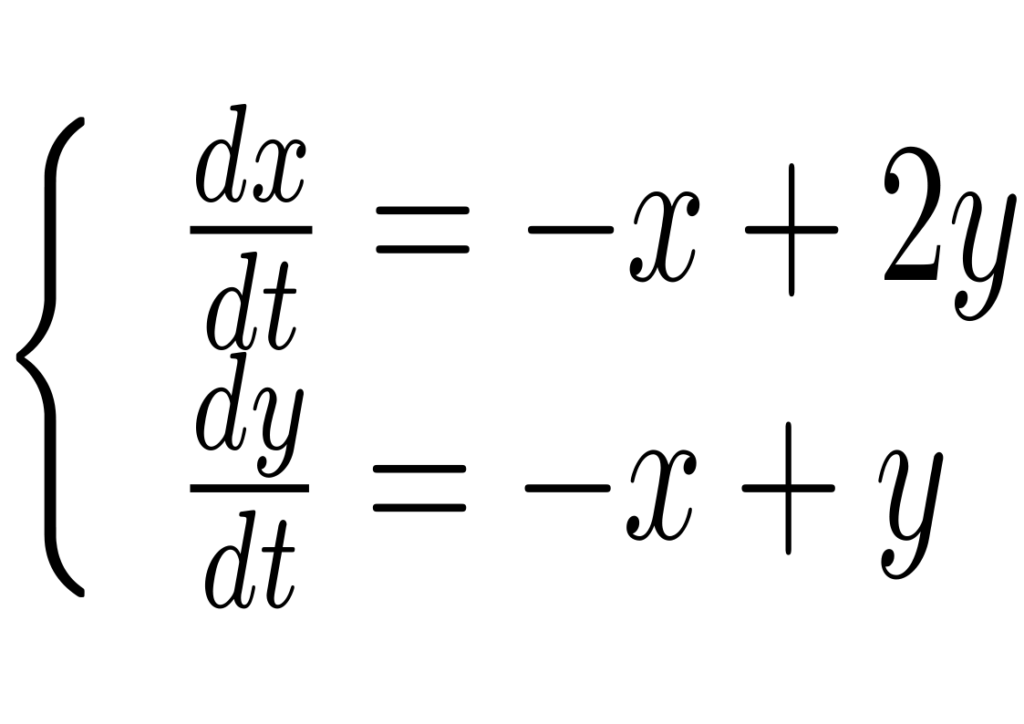
A matriz correspondente ao sistema possui autovalores complexos dados por i e -i, o autovetor associado ao autovalor i é (1-i,1). Logo a solução geral é dada por
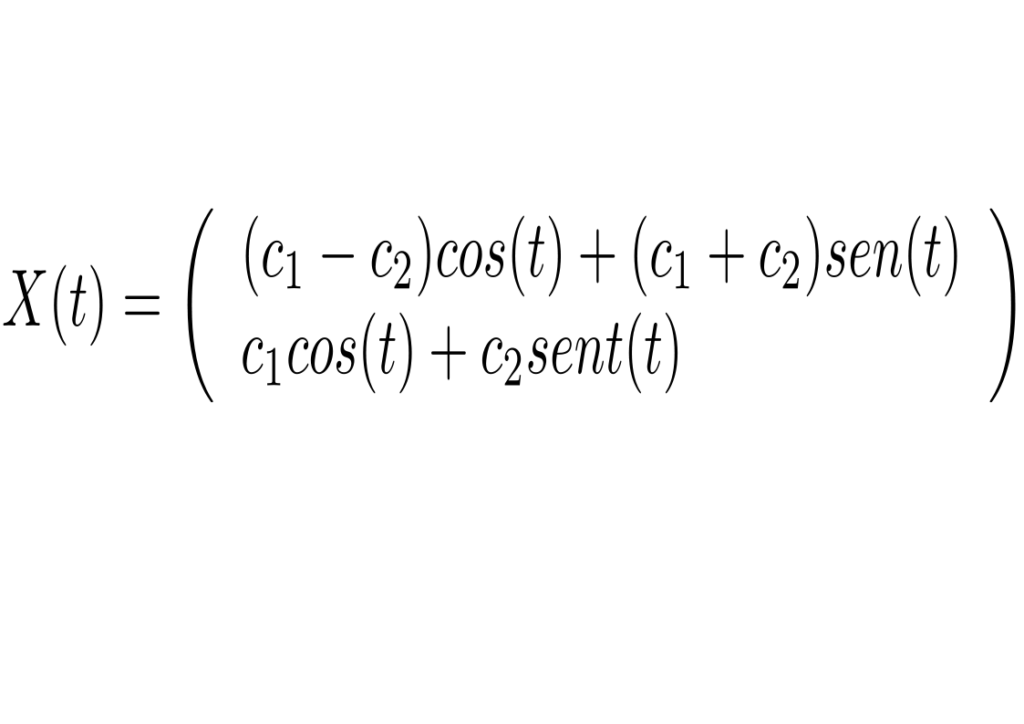
Com a condição inicial X(0)=(1,0), temos que
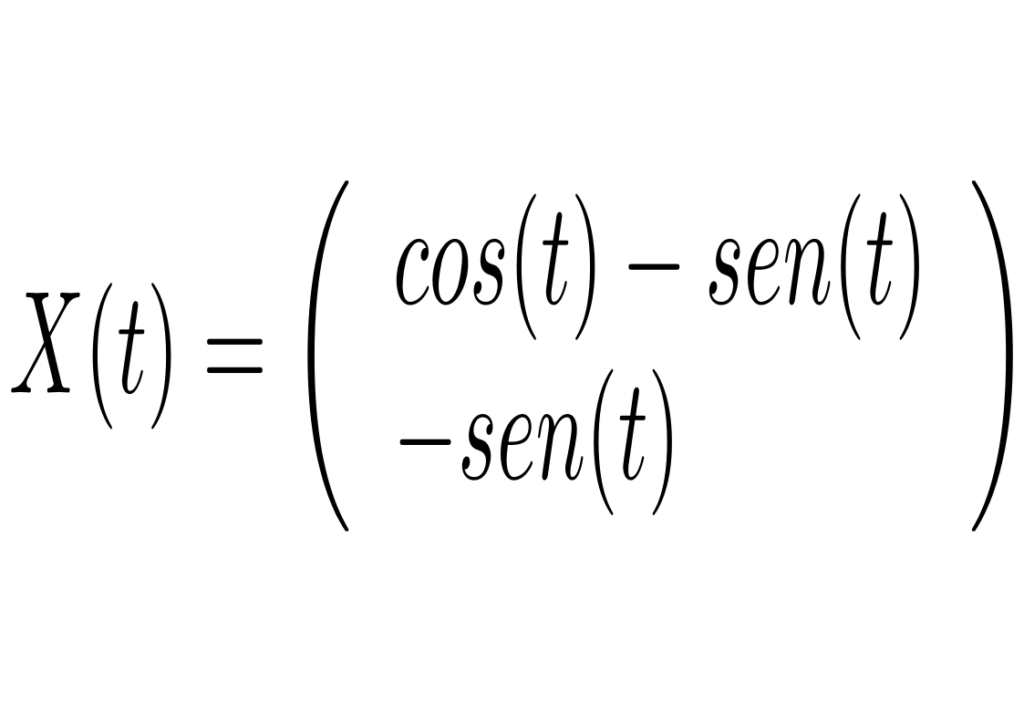
com a dinâmica
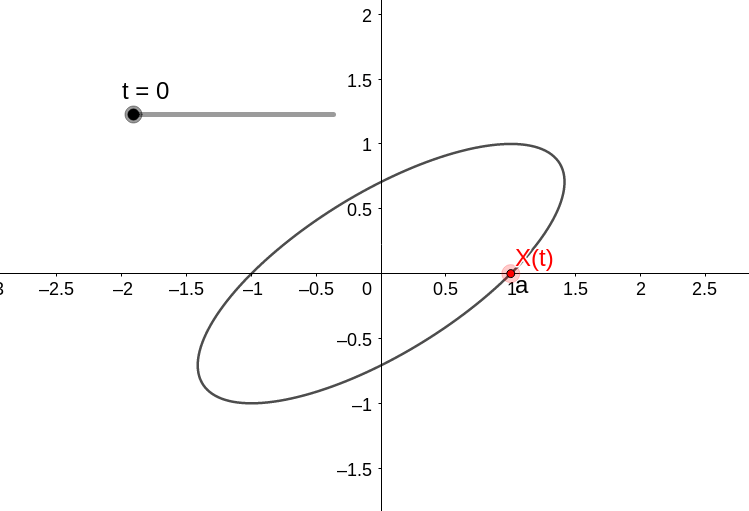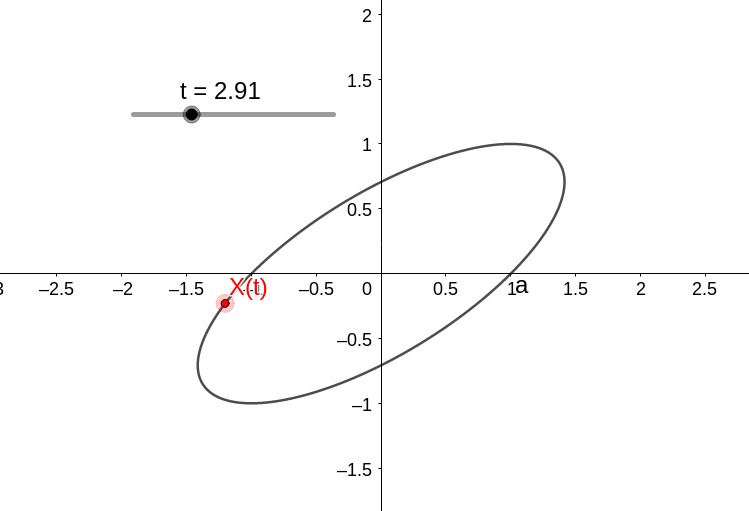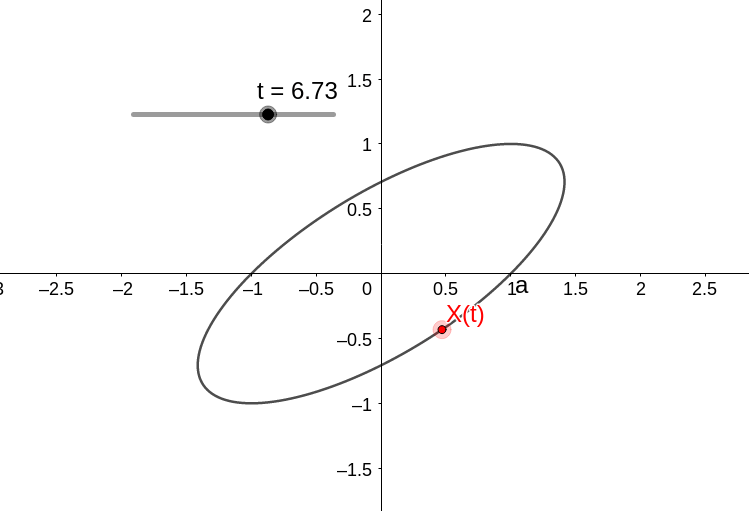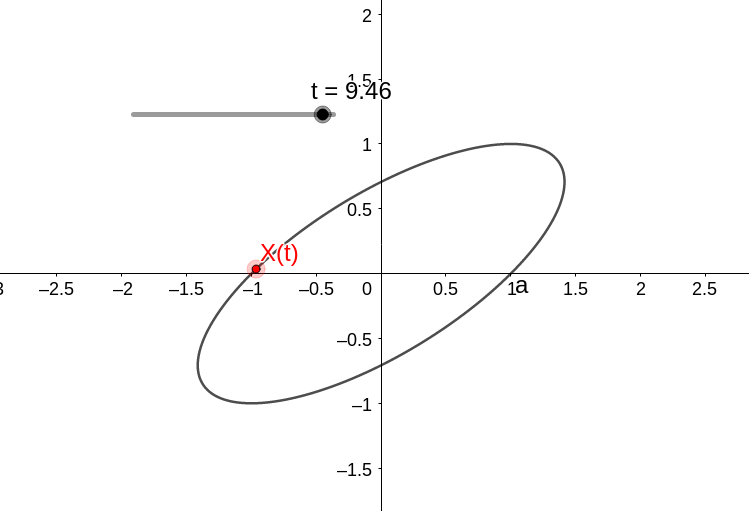
Agora consideremos o sistema
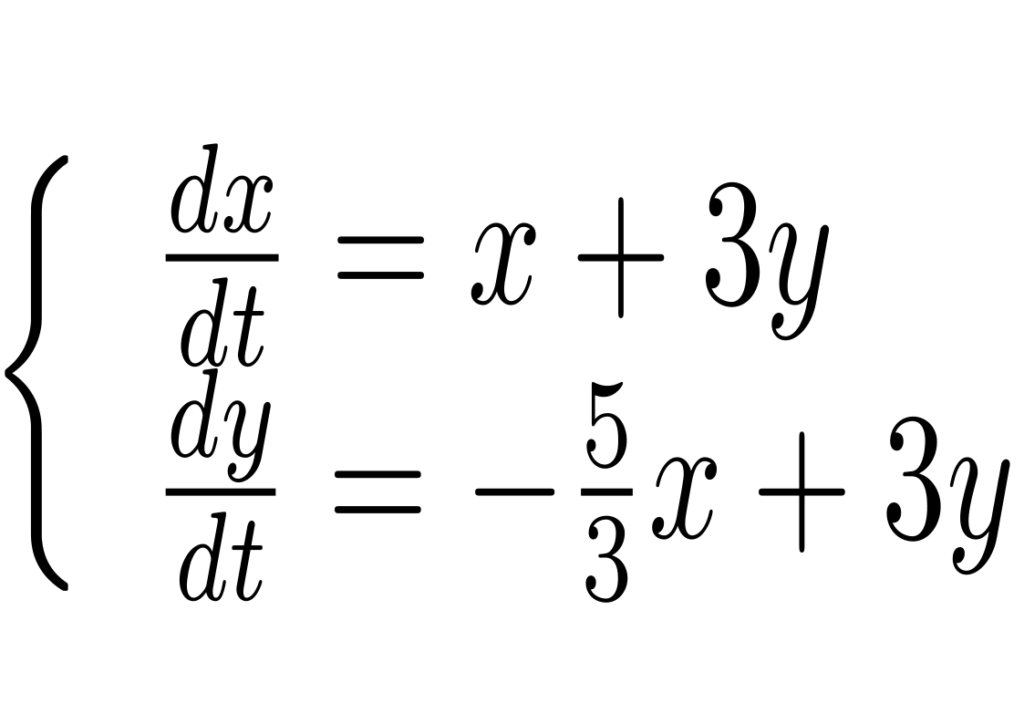
A matriz correspondente ao sistema possui autovalores complexos dados por 2+2i e 2-2i, o autovetor associado ao autovalor 2+2i é (1,1+2i). Logo a solução geral é dada por
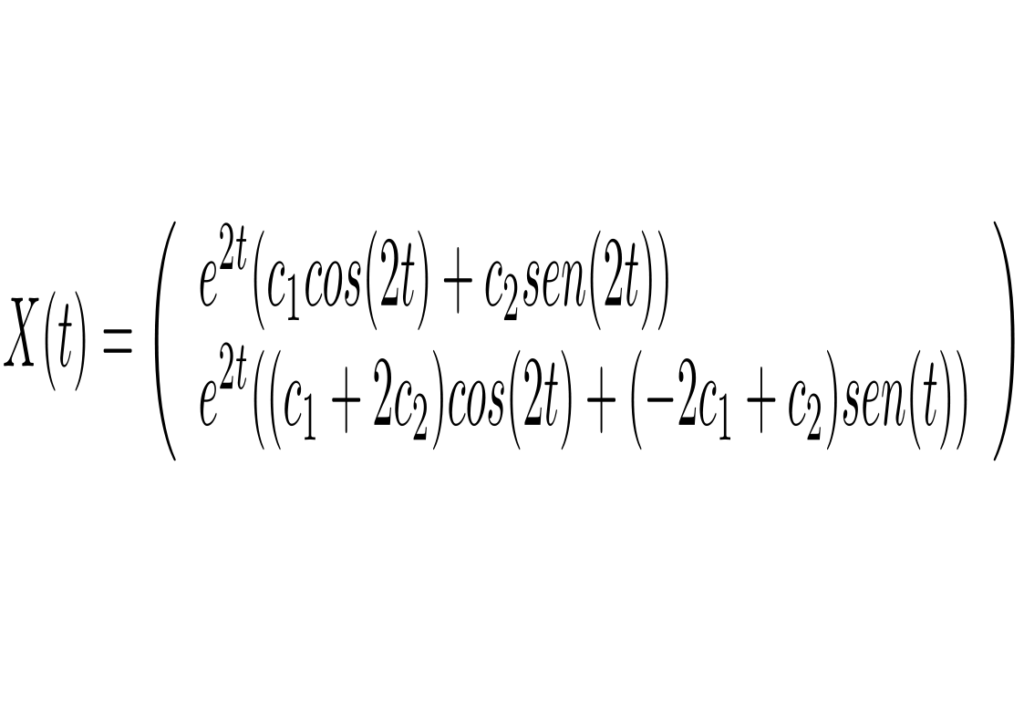
Com a condição inicial X(0)=(1,0), temos que
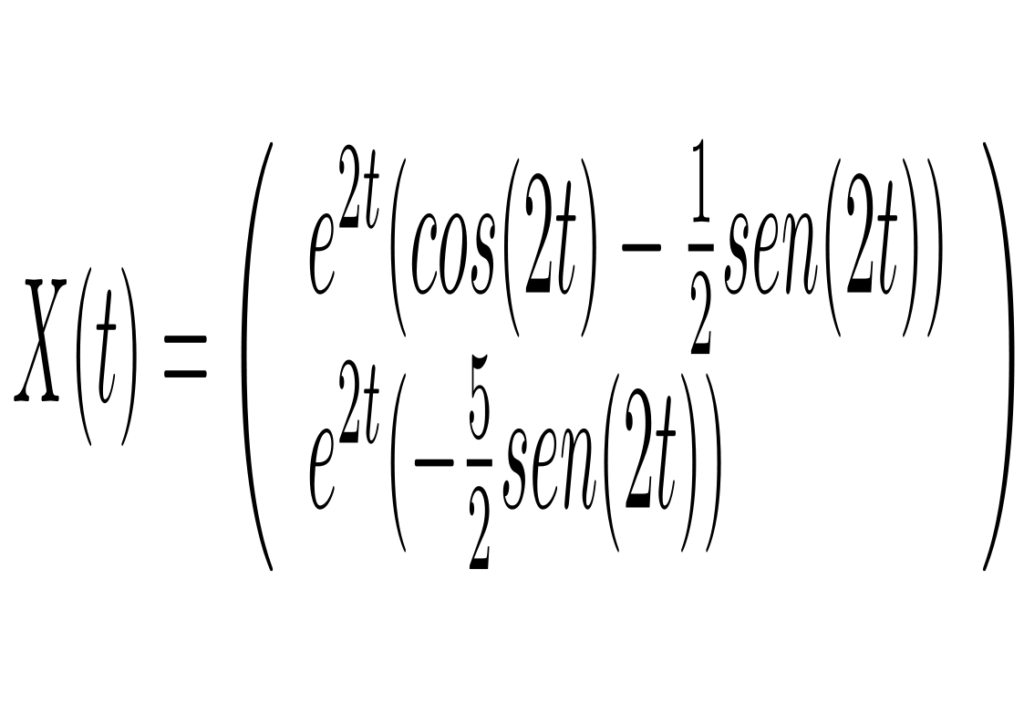
com a dinâmica
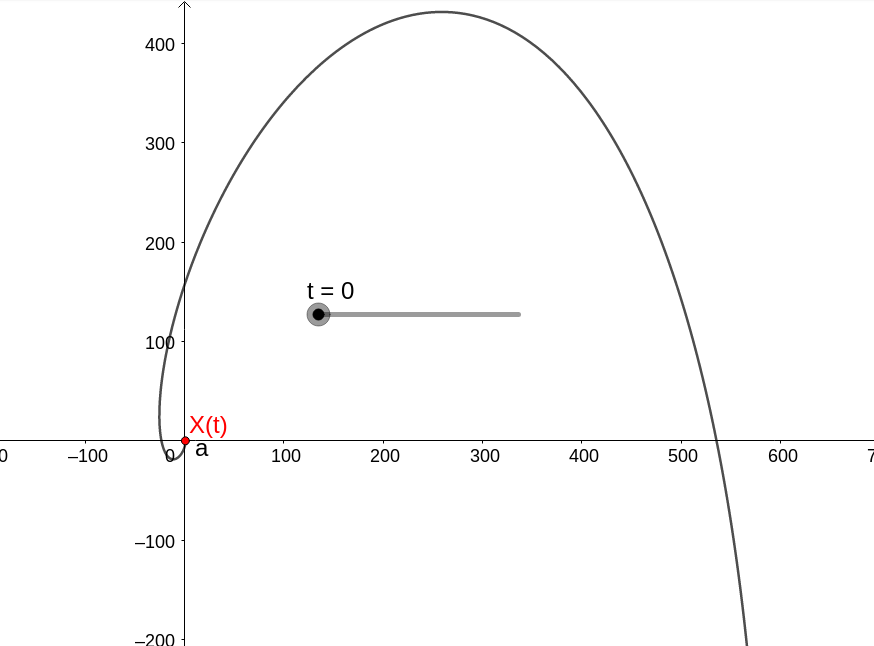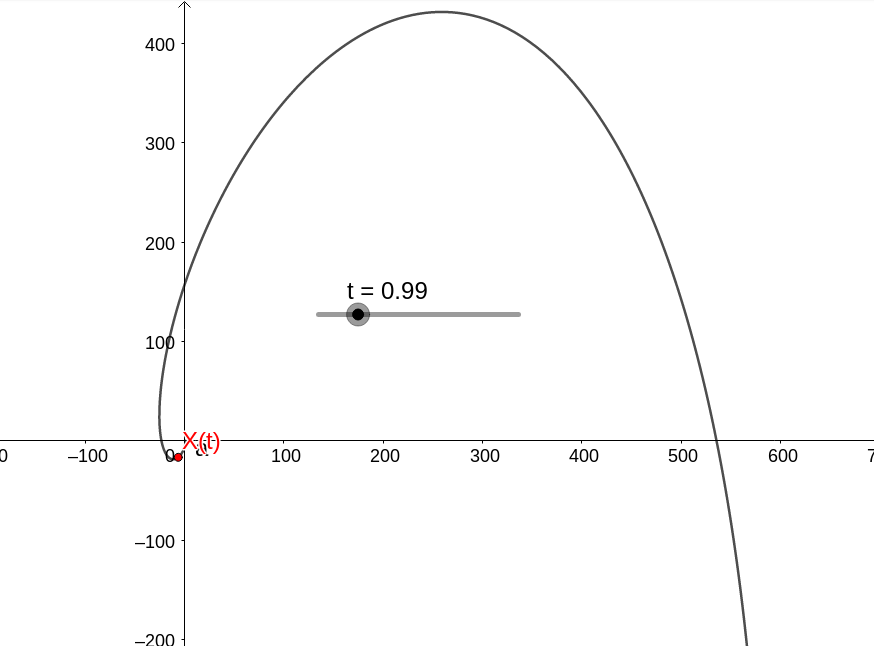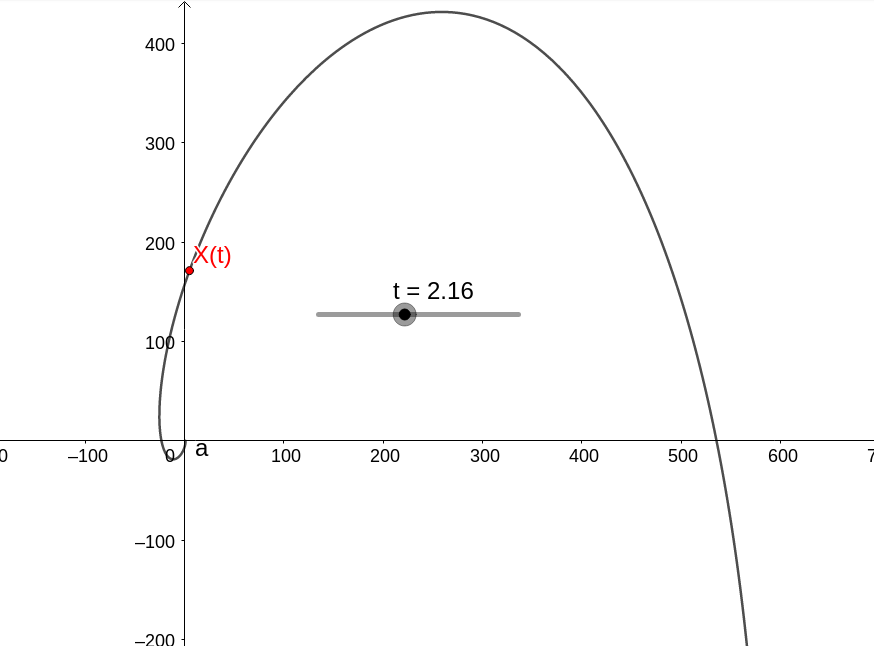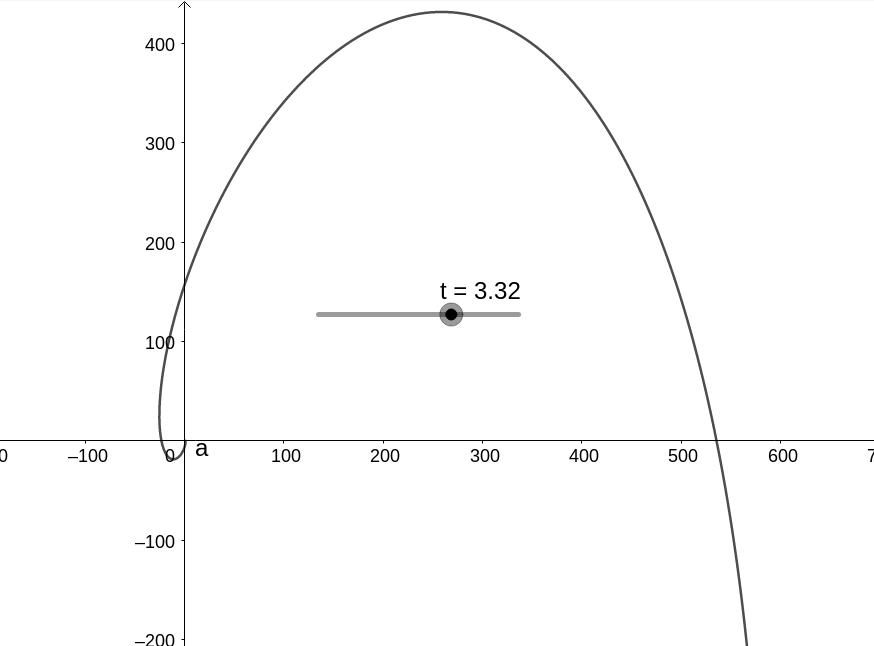
Para o próximo exemplo, considere o sistema
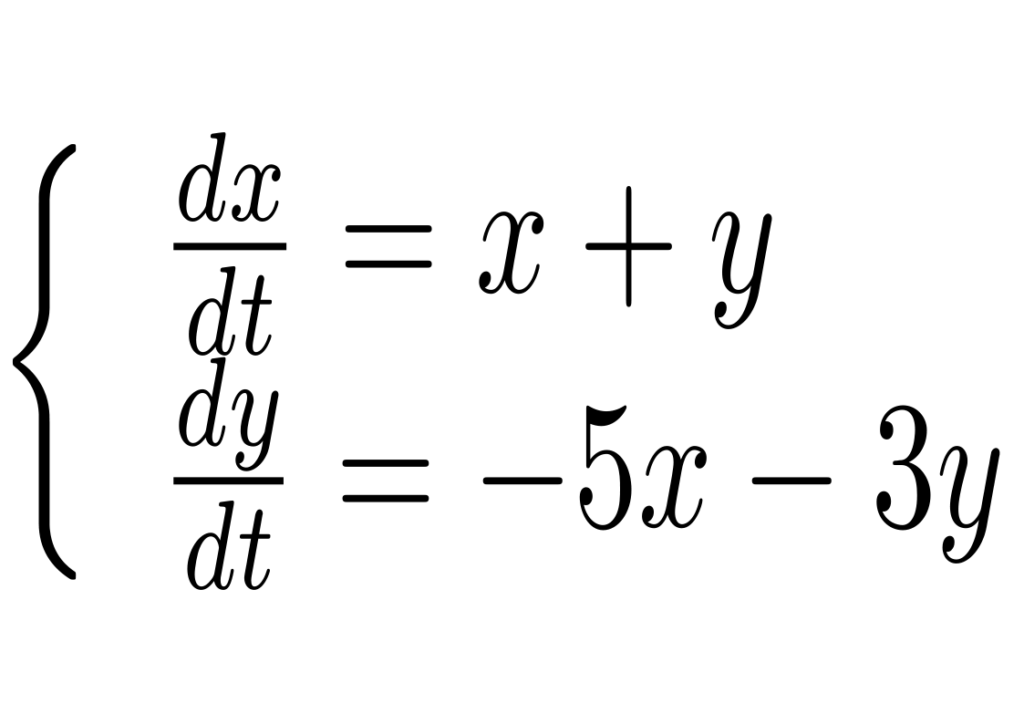
A matriz correspondente ao sistema possui autovalores complexos dados por -1+i e -1-i, o autovetor associado ao autovalor -1+i é (-2/5-i/5,1). Logo a solução geral é dada por
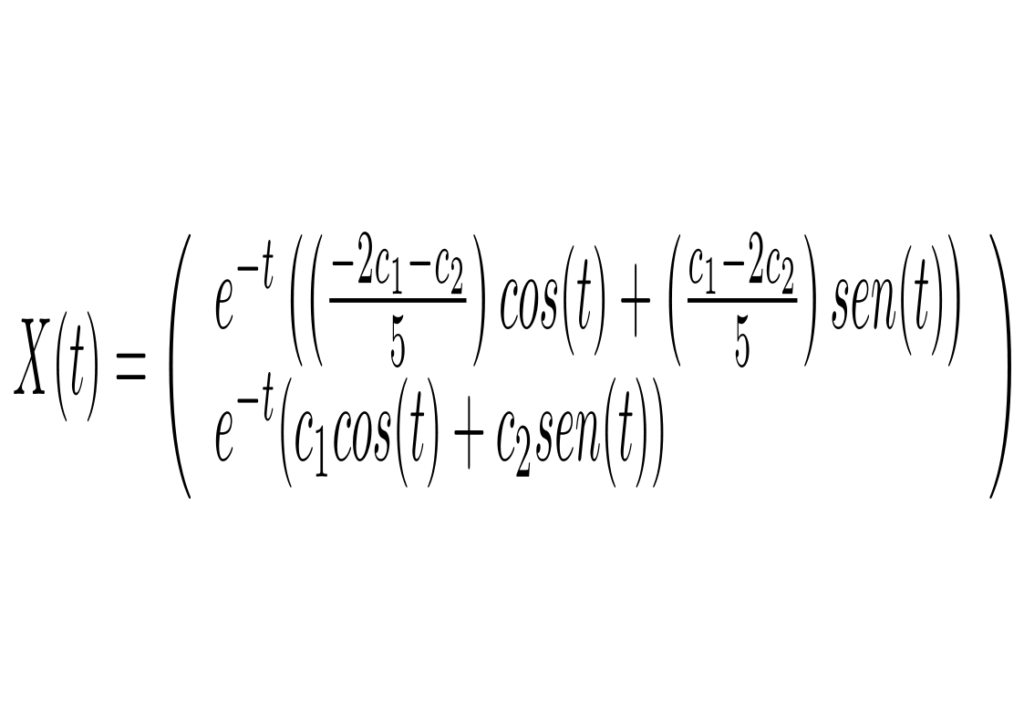
Com a condição inicial X(0)=(1,0), temos que
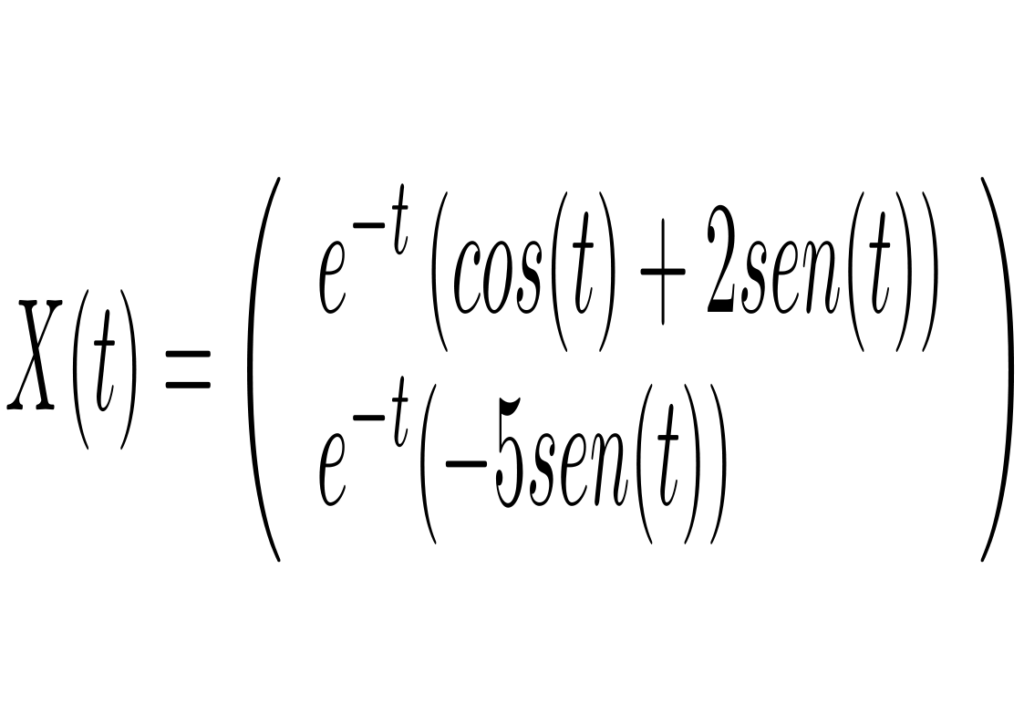
com a dinâmica